
����Ŀ����ͼ����֪�����߾���A��1��0����B��0��3�����㣬�Գ�����x=��1 
��1���������߶�Ӧ�ĺ�����ϵʽ��
��2������Q�ӵ�O��������ÿ��1����λ���ȵ��ٶ����߶�OM���˶���ͬʱ����M��M��O�������ÿ��3����λ���ȵ��ٶ����߶�OB���˶�������Q��x��Ĵ��߽��߶�AB�ڵ�N�����������ڵ�P�����˶���ʱ��Ϊt�룮
�ٵ�tΪ��ֵʱ���ı���OMPQΪ���Σ�
�ڡ�AON�ܷ�Ϊ���������Σ����ܣ�ֱ��д��t��ֵ�������ܣ���˵�����ɣ�
���𰸡�
��1��
�⣺�������⣬�������ߵĽ���ʽΪ��y=a��x+1��2+k��
�ߵ�A��1��0����B��0��3�����������ϣ�
�� ![]() ��
��
��ã�a=��1��k=4��
�������ߵĽ���ʽΪ��y=����x+1��2+4=��x2��2x+3��
��2��
�⣺�١��ı���OMPQΪ���Σ�
��OM=PQ����3t=����t+1��2+4��
�����ã�t2+5t��3=0��
���t= ![]() ������t=
������t= ![]() ��0������ȥ��
��0������ȥ��
�൱t= ![]() ��ʱ���ı���OMPQΪ���Σ�
��ʱ���ı���OMPQΪ���Σ�
���ܣ�Rt��AOB�У�OA=1��OB=3����tanA=3��
����AON���������������������
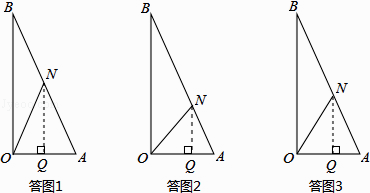
��I����ON=AN�����ͼ1��ʾ��
��QΪOA�е㣬OQ= ![]() OA=
OA= ![]() ��
��
��t= ![]() ��
��
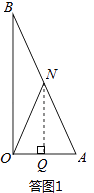
��II����ON=OA�����ͼ2��ʾ��
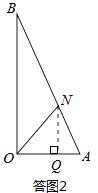
��AQ=x����NQ=AQtanA=3x��OQ=OA��AQ=1��x��
��Rt��NOQ�У��ɹ��ɶ����ã�OQ2+NQ2=ON2��
����1��x��2+��3x��2=12�����x1= ![]() ��x2=0����ȥ����
��x2=0����ȥ����
��x= ![]() ��OQ=1��x=
��OQ=1��x= ![]() ��
��
��t= ![]() ��
��
��III����OA=AN�����ͼ3��ʾ��

��AQ=x����NQ=AQtanA=3x��
��Rt��ANQ�У��ɹ��ɶ����ã�NQ2+AQ2=AN2��
����x��2+��3x��2=12�����x1= ![]() ��x2=��
��x2=�� ![]() ����ȥ����
����ȥ����
��OQ=1��x=1�� ![]() ��
��
��t=1�� ![]() ��
��
��tΪ ![]() �롢
�롢 ![]() �룬��1��
�룬��1�� ![]() ����ʱ����AONΪ���������Σ�
����ʱ����AONΪ���������Σ�
����������1�����ö���ʽ������ϵ������������ߵĽ���ʽ����2���ٵ��ı���OMPQΪ����ʱ����������OM=PQ���ݴ���һԪ���η�����⣻�ڡ�AONΪ����������ʱ�����ܴ����������Σ���Ҫ�������ۣ���һ���㣮
�����㾫�������յ��������ε������ǽ����ĸ�������Ҫ֪�����������ε���������ȣ���ƣ��ȱ߶ԵȽǣ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���߳�Ϊ2��������ABCD�У�E��BA�ӳ�����һ�㣬��AE=AB����P�ӵ�D��������ÿ��1����λ������D��CB���յ�B�˶���ֱ��EP��AD�ڵ�F������F��ֱ��FG��DE�ڵ�G����AB�ڵ�R.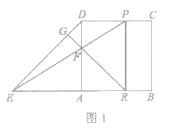

��1����֤��AF=AR;
��2�����P�˶���ʱ��Ϊt�룬��ѡtΪ��ֵʱ���ı���PRBC�Ǿ��Σ�
��3����ͼ2������PB����ֱ��д��ʹ��PRB�ǵ���������ʱt��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У���BAD=120�㣬��B=��D=90�㣬��BC��CD�Ϸֱ���һ��M��N��ʹ��AMN�ܳ���Сʱ�����AMN+��ANM�Ķ����� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC��AD��BC���ϵ����ߣ���ADΪֱ������O������BO���ӳ�����E��ʹ��OE=OB������O�ڵ�F������AE��CE�� 
��1����֤��AE�ǡ�O�����ߣ�
��2����֤���ı���ADCE�Ǿ��Σ�
��3����BD= ![]() AD=4������Ӱ���ֵ������
AD=4������Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊ2��������MNEF���ĸ�������ڴ�ԲO�ϣ�СԲO�������θ��߶����У�AB��CD�Ǵ�ԲO��ֱ����AB��CD��CD��MN��С��������ˮƽ���õĸ�Բ����������һ��С����С��ͣ�ڸ�ͼ����Ӱ��������ĸ���Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ1��AC��BD�ǶԽ��ߣ�����DCB���ŵ�D˳ʱ����ת45��õ���DGH��HG��AB�ڵ�E������DE��AC�ڵ�F������FG�������н��ۣ�
���ı���AEGF������
�ڡ�AED�ա�GED
�ۡ�DFG=112.5��
��BC+FG=1.5
������ȷ�Ľ����� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������y=x2+bx+c��A��B��C���㣬��A�������ǣ�3��0������C�������ǣ�0����3��������P���������ϣ�
��1��b= �� c= �� ��B������Ϊ����ֱ����д�����
��2���Ƿ���ڵ�P��ʹ�á�ACP����ACΪֱ�DZߵ�ֱ�������Σ������ڣ�������з��������ĵ�P�����ꣻ�������ڣ�˵�����ɣ�
��3��������P��PE��ֱy���ڵ�E����ֱ��AC�ڵ�D������D��x��Ĵ��ߣ�����ΪF������EF�����߶�EF�ij������ʱ�������P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С÷�ҵ���̨�Ϸ�����һ��ɹ�¼���ͼ1��ͼ2��ɹ�¼ܵIJ���ʾ��ͼ��A��B�������ڵ��棬��ɹ�¼��ȹ��ſ�������Žǡ�AOB=62�㣬����OA=OB=140cm��С÷������ȹ�����¼ܺ���ܳ���Ϊ122cm���ʽ��������ȹ������ɹ�¼����Ƿ�����䵽���棿��ͨ������˵�����ɣ��ο����ݣ�sin59���0.86��cos59���0.52��tan59���1.66��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���¶��壺ֱ��l1��l��l2 �� �ཻ�ڵ�O����Ϊm���߶�AB��ֱ��l2�ϣ���P��ֱ��l1��һ�㣬��Q��ֱ��l��һ�㣮����AQB=2��APB�������dzƵ�P�ǵ�Q�İ��µ㣻
��1����ͼ1��ֱ��l2��l�ļн�Ϊ30�㣬�߶�AB�ڵ�O�Ҳ࣬��OA=1��m=2����Ҫʹ�á�APB=45���������P�ǵ�Q�İ��µ㣬��OQ= 
��2����ͼ2����ֱ��l1��l2�ļн�Ϊ60�㣬��m=3����Ҫʹ�á�APB=30�㣬�߶�AB��ֱ��l2�������ƶ���
�ٵ�OA�ij�Ϊ����ʱ�����������İ��µ�P����ֻ��һ������˵�����ɣ�
���Ƿ���ڷ��������İ��µ�P������������������ڣ���ֱ��д��OA�����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com