Question

求所有的正整数m，n使得m²+1是一个质数，且10（m²+1）=n²+1．

Answer 1

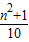
【答案】分析：首先根据质数的定义得出n²的个位数必是9，这样的数是个位有3，或7的数且也是质数，分别带入特殊数求出即可．
解答：解：由题意m²+1是质数，所以m²+1的值是2，3，5，7，11，13，17，19…，
则m=1，，2，…
符合题意的有：m=2，4，
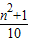
而10（m²+1）=n²+1，则说明n²的个位数必是9，这样的数是个位有3，或7的数，且也是质数，
只有当m=2，则n=7；当m=4，则n=13符合题意，
故符合要求的有：（2，7）或者（4，13）．
点评：此题主要考查了质数的性质，根据已知得出m的值是解题关键．