
 如图,AD⊥BC,垂足为D,BE⊥AC,垂足为E,AD与BE相交于点F,连接ED.
如图,AD⊥BC,垂足为D,BE⊥AC,垂足为E,AD与BE相交于点F,连接ED.科目:初中数学 来源: 题型:填空题
 如图,已知△ABC,按如下步骤作图:①以A为圆心,AB长为半径画弧;②以C为圆心,CB长为半径画弧,两弧相交于点D;③连结AD,CD.则△ABC≌△ADC的依据是SSS.
如图,已知△ABC,按如下步骤作图:①以A为圆心,AB长为半径画弧;②以C为圆心,CB长为半径画弧,两弧相交于点D;③连结AD,CD.则△ABC≌△ADC的依据是SSS.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
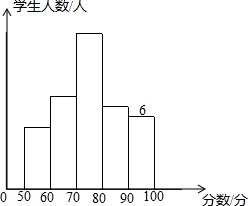 某校同学参加语文知识竞赛,将学生的成绩,进行整理后分成5组,绘制成频数分布直方图如下,图中从左到右各小组的频率分别是0.0625,0.25,0.375,0.1875,0.125且已知最右边小组的频数为6,结合直方图提供的信息,解答下列问题:
某校同学参加语文知识竞赛,将学生的成绩,进行整理后分成5组,绘制成频数分布直方图如下,图中从左到右各小组的频率分别是0.0625,0.25,0.375,0.1875,0.125且已知最右边小组的频数为6,结合直方图提供的信息,解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com