
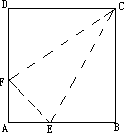
 如图,小明将一张矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=3:5,求sin∠DCF的值是( )
如图,小明将一张矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=3:5,求sin∠DCF的值是( )科目:初中数学 来源: 题型:
| 5 |

查看答案和解析>>
科目:初中数学 来源:学习周报 数学 北师大九年级版 2009-2010学年 第15期 总第171期 北师大版 题型:022
如图,小明将一张矩形纸片ABCD沿CE折叠,使点B恰好落在AD上,设此点为F,若AB∶BC=4∶5,则cos∠DCF的值是________.

查看答案和解析>>
科目:初中数学 来源:中考必备’04全国中考试题集锦·数学 题型:022
如图,小明将一张矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB∶BC=4∶5,则cos∠DCF的值是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com