2011
分析:由已知的第一个等式移项得出a
2=-4a-1,将第二个等式去分母整理后,把a
2=-4a-1代入,化简整理后再把a
2=-4a-1代入,整理后根据多项式为0时满足的条件列出关于m的方程,求出方程的解即可得到m的值.
解答:由a
2+4a+1=0,得到a
2=-4a-1,
将
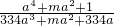
=3变形得:a
4+ma
2+1=1002a
3+3ma
2+1002a,
整理得:a
2(a
2-2m)-1002a(a
2+1)+1=0,
即(-4a-1)(-4a-1-2m)-1002a(-4a-1+1)+1=0,
整理得:4024a
2+(8+8m)a+2m+2=0,
即4024(-4a-1)+(8+8m)a+2m+2=0,
整理得:(-16088+8m)a+2m-4022=0,
可得-16088+8m=0,且2m-4022=0,
解得:m=2011.
故答案为:2011
点评:此题考查了分式的化简求值,利用了整体代入及降次的思想,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式,约分时分式分子分母出现多项式,应先将多项式分解因式后再约分.将已知等式合理的变形是解本题的关键.

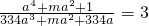 ,则m=________.
,则m=________.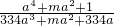 =3变形得:a4+ma2+1=1002a3+3ma2+1002a,
=3变形得:a4+ma2+1=1002a3+3ma2+1002a,

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案