建筑“津合”高速公路经过某村,需搬迁一批农户,为了节约土地资源和保护环境,政府统一规划搬迁区域,规划要求区域内绿化环境占地面积不少于区域总面积的30%,若搬迁农户建房每户占地100m2,则绿化环境面积还占总面积的45%;政府又鼓励其他有积蓄的农户到规划区域建房,这样又有20户农户加入建房,若仍以每户占地100m2计算,则这时绿化环境面积又占总面积的25%,为了符合规划要求,又需要退出部分农户.
问(1)最初需搬迁建房的农户有多少户?政府规划的建房区域总面积是多少m2?
(2)为了保证绿化环境占地面积不少于区域总面积的30%,至少需退出农户几户?
【答案】
分析:(1)设最初需搬迁建房的农户有x户,规划的建房区域面积为ym
2,规划要求区域内绿化环境占地面积不少于区域总面积的30%,若搬迁农户建房每户占地100m
2,则绿化环境面积还占总面积的45%;政府又鼓励其他有积蓄的农户到规划区域建房,这样又有20户农户加入建房,若仍以每户占地100m
2计算,则这时绿化环境面积又占总面积的25%,可列出方程组求解.
(2)设至少需退出农户a户,根据保证绿化环境占地面积不少于区域总面积的30%,可列不等式求解.
解答:解:(1)设最初需搬迁建房的农户有x户,规划的建房区域面积为ym
2,
由题意得
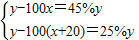
(4分)
解得
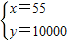
(6分)
(2)设需退出农户a户,则
10000-100(55+20-a)≥30%•10000(8分)
解得a≥5(9分)
答:(1)最初需搬迁建房的农户有55户,政府规划的建房区域总面积是10000m
2(2)至少需退出农户5户(10分)
点评:本题考查二元一次方程组的应用和一元一次不等式的应用,根据题意以绿化面积做为等量关系列出方程组,求出规划的建房区域面积和搬迁建房的农户,根据绿化环境占地面积不少于区域总面积的30%,列出不等式求出需要搬出的几户.

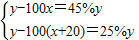 (4分)
(4分)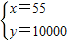 (6分)
(6分)

 阅读快车系列答案
阅读快车系列答案