
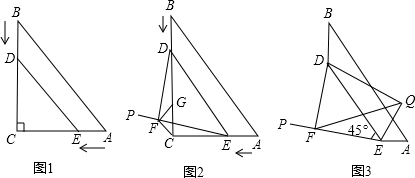
分析 (1)由题意知AE=BD=t,所以EC=15-t,DC=20-t,代入DC-EC中即可求出它的值,另外S=$\frac{1}{2}$EC•DC,分别将DC和EC代入即可求出S与t的函数关系式;
(2)容易求出△ABC的面积,令(1)的函数解析式中的S=75,即可求出t的值,要注意t的范围;
(3)延长AC至H使得,CH=GC=5,连接HF,利用条件易证△HEF≌△CDF,所以HF=CF,∠FHE=∠FCD,即可证明△HFC是等腰直角三角形,从而可知CF=$\frac{\sqrt{2}}{2}$CH;
(4)延长QD至点G,使得DG=QE,连接GF,易证△GDF≌△QEF,所以GF=QF,∠GFD=∠QFE,从而可证明△GFQ是等腰直角三角形,所以FQ=$\frac{\sqrt{2}}{2}$QG=$\frac{\sqrt{2}}{2}$(DG+DQ)=$\frac{\sqrt{2}}{2}$(m+n).
解答 解:(1)由题意知:AE=BD=t,
∴EC=15-t,DC=20-t,
∴DC-EC=(20-t)-(15-t)=5,
∴S=$\frac{1}{2}$EC•DC
=$\frac{1}{2}$(15-t)(20-t)
=$\frac{{t}^{2}}{2}$-$\frac{35t}{2}$+150
故答案为:5;
(2)△ABC的面积为$\frac{1}{2}$×20×15=150,
当S=$\frac{1}{2}$×150时,
∴$\frac{{t}^{2}}{2}$-$\frac{35t}{2}$+150=75,
解得:t=5或t=30,
∵0≤t<15,
∴t=5,
∴BD=t=5,
∴点D运动到$\frac{1}{4}$BD处时,S等于△ABC面积的一半;
(3)延长AC至H使得,CH=GC=5,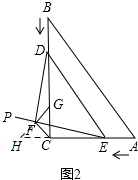
连接HF,如图2,
由(1)可知,DC-EC=5,
即DC-EC=CH,
∴DC=EC+CH=EH,
∵DF⊥EF,∠DEF=45°,
∴△DFE是等腰直角三角形,
∴DF=EF,
∵∠DFE=∠DCE=90°,
∴F、C、E、D四点共圆,
∴∠FDC=∠FEH,
在△HEF与△CDF中,
$\left\{\begin{array}{l}{EF=DF}\\{∠FEH=∠FDC}\\{HE=CD}\end{array}\right.$,
∴△HEF≌△CDF(SAS),
∴HF=CF,∠FHE=∠FCD,
∵HF=CF,
∴∠FHE=∠FCH,
∴∠FCH=∠FCD,
∵∠HCB=90°,
∴∠FCH=∠FCD=45°,
∴△HFC是等腰直角三角形,
∴CF=$\frac{\sqrt{2}}{2}$CH=$\frac{5\sqrt{2}}{2}$;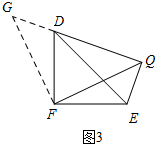
(4)延长QD至点G,使得DG=QE,
连接GF,
∵∠DFE=∠DQE=90°,
∴∠FDQ+∠FEQ=180°,
∵∠GDF+∠FDQ=180°,
∴∠GDF=∠QEF,
由(3)可知:△DFE是等腰直角三角形,
∴DF=EF,
在△GDF与△QEF中,
$\left\{\begin{array}{l}{GD=QE}\\{∠GDF=∠QEF}\\{DF=EF}\end{array}\right.$
∴△GDF≌△QEF(SAS),
∴GF=QF,∠GFD=∠QFE,
∴∠DFQ+∠QFE=∠DFQ+∠GFD,
∴∠DFE=∠GFQ=90°,
∴△GFQ是等腰直角三角形,
∴FQ=$\frac{\sqrt{2}}{2}$QG=$\frac{\sqrt{2}}{2}$(DG+DQ)=$\frac{\sqrt{2}}{2}$(m+n).
点评 本题考查几何变换综合问题,涉及全等三角形的性质与判定,等腰直角三角形的判定与性质,旋转性质等知识内容,内容较为综合,需要学生综合运用所学知识解决.


科目:初中数学 来源: 题型:填空题
 如图,在菱形ABCD中,AB=2,∠DAB=60°,连对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°,连结E,再以AE为边作第三个作菱形AEGH,使∠HAE=60°,…按此规律所作的第2014个菱形的边长是2×($\sqrt{3}$)2013.
如图,在菱形ABCD中,AB=2,∠DAB=60°,连对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°,连结E,再以AE为边作第三个作菱形AEGH,使∠HAE=60°,…按此规律所作的第2014个菱形的边长是2×($\sqrt{3}$)2013.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 距离地面高度(千米)h | 0 | 1 | 2 | 3 | 4 | 5 |
| 温度(℃)t | 20 | 14 | 8 | 2 | -4 | -10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 湖产品种类 | A类 | B类 | C类 |
| 每辆汽车装载吨数 | 2 | 1 | 1.5 |
| 每吨湖产品可获利润(万元) | 5 | 7 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知AB∥CD,AD是∠CAB的平分线且交CD于点D.
如图,已知AB∥CD,AD是∠CAB的平分线且交CD于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一块矩形木板ABCD,长AD=3cm,宽AB=2cm,小虎将一块等腰直角三角板的一条直角边靠在顶点C上,另一条直角边与AB边交于点E,三角板的直角顶点P在AD边上移动(不含端点A、D),当线段BE最短时,AP的长为( )
一块矩形木板ABCD,长AD=3cm,宽AB=2cm,小虎将一块等腰直角三角板的一条直角边靠在顶点C上,另一条直角边与AB边交于点E,三角板的直角顶点P在AD边上移动(不含端点A、D),当线段BE最短时,AP的长为( )| A. | $\frac{1}{2}$cm | B. | 1cm | C. | $\frac{3}{2}$cm | D. | 2cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,∠DAB=∠BCD=90°,点E是BD上任意一点,点O是AC的中点,AF∥EC交EO的延长线于点 F,连接AE,CF.
如图,在四边形ABCD中,∠DAB=∠BCD=90°,点E是BD上任意一点,点O是AC的中点,AF∥EC交EO的延长线于点 F,连接AE,CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC.
如图,已知△ABC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com