
【题目】如图1,在△ABO中,∠OAB=90°,∠AOB=30°,OB=8.以OB为一边,在△OAB外作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E.
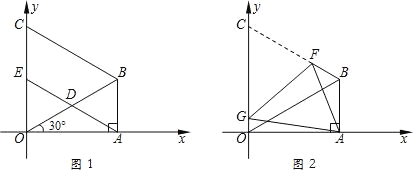
(1)求点B的坐标;
(2)求证:四边形ABCE是平行四边形;
(3)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
【答案】(1)(4![]() ,4)(2)证明见解析(3)1
,4)(2)证明见解析(3)1
【解析】
试题分析:(1)由在△ABO中,∠OAB=90°,∠AOB=30°,OB=8,根据三角函数的知识,即可求得AB与OA的长,即可求得点B的坐标;
(2)首先可得CE∥AB,D是OB的中点,根据直角三角形斜边的中线等于斜边的一半,可证得BD=AD,∠ADB=60°,又由△OBC是等边三角形,可得∠ADB=∠OBC,根据内错角相等,两直线平行,可证得BC∥AE,继而可得四边形ABCD是平行四边形;
(3)首先设OG的长为x,由折叠的性质可得:AG=CG=8﹣x,然后根据勾股定理可得方程(8﹣x)2=x2+(4![]() )2,解此方程即可求得OG的长.
)2,解此方程即可求得OG的长.
试题解析:(1)在△OAB中,∠OAB=90°,∠AOB=30°,OB=8,
∴OA=OBcos30°=8×![]() =4
=4![]() ,
,
AB=OBsin30°=8×![]() =4,
=4,
∴点B的坐标为(4![]() ,4);
,4);
(2)∵∠OAB=90°,
∴AB⊥x轴,
∵y轴⊥x轴,
∴AB∥y轴,即AB∥CE,
∵∠AOB=30°,
∴∠OBA=60°,
∵DB=DO=4
∴DB=AB=4
∴∠BDA=∠BAD=120°÷2=60°,
∴∠ADB=60°,
∵△OBC是等边三角形,
∴∠OBC=60°,
∴∠ADB=∠OBC,
即AD∥BC,
∴四边形ABCE是平行四边形;
(3)设OG的长为x,
∵OC=OB=8,
∴CG=8﹣x,
由折叠的性质可得:AG=CG=8﹣x,
在Rt△AOG中,AG2=OG2+OA2,
即(8﹣x)2=x2+(4![]() )2,
)2,
解得:x=1,
即OG=1.


科目:初中数学 来源: 题型:
【题目】某电脑公司经销甲种型号电脑,受经济危机影响,电脑价格不断下降.今年三月份的电脑售价比去年同期每台降价1000元,如果卖出相同数量的电脑,去年销售额为10万元,今年销售额只有8万元.
(1)今年三月份甲种电脑每台售价多少元?
(2)为了增加收入,电脑公司决定再经销乙种型号电脑,已知甲种电脑每台进价为3500元,乙种电脑每台进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台,有几种进货方案?
(3)如果乙种电脑每台售价为3800元,为打开乙种电脑的销路,公司决定每售出一台乙种电脑,返还顾客现金a元,要使(2)中所有方案获利相同,a值应是多少此时,哪种方案对公司更有利?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定个人发表文章、出版图书获得稿费的纳税计算办法是:(1)稿费不高于800元的不纳税;(2)稿费高于800元又不高于4 000元的应缴纳超过800元的那一部分稿费的14%的税;(3)稿费高于4 000元的应缴纳全部稿费的11%的税.今知丁老师获得一笔稿费,并缴纳个人所得税420元,则丁老师的这笔稿费有________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a=12.3是由四舍五入得到的近似数,则a的可能取值范围是( )
A. 12.25≤a≤12.35 B. 12.25≤a<12.35
C. 12.25<a≤12.35 D. 12.25<a<12.35
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某产品每件成本为10元,试销阶段的售价x(元)与销售利润y(元)满足y=(x﹣10)(40﹣x),那么获利最多时的售价为( )
A. 10元 B. 25元 C. 40元 D. 55元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com