
 DE;
DE; CF,AE=6,求GH的长.
CF,AE=6,求GH的长.
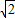 DE;
DE;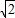 EC,设EC=x,则DE=
EC,设EC=x,则DE=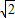 x,由(1)结论可得:6-x=2x,则可求得DE等线段的长度,又由△ADH≌△CDB,可求得DH与CA的长,然后过F做FM∥AE交CD于点M,由相似三角形的对应边成比例,即可求得GH的长.
x,由(1)结论可得:6-x=2x,则可求得DE等线段的长度,又由△ADH≌△CDB,可求得DH与CA的长,然后过F做FM∥AE交CD于点M,由相似三角形的对应边成比例,即可求得GH的长.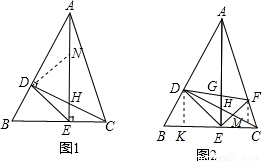 解:(1)过点D作DN⊥DE交AE于点N.
解:(1)过点D作DN⊥DE交AE于点N.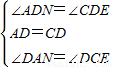 ,
, DE,
DE,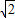 DE;
DE;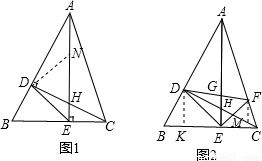
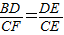 ,
,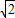 CF,
CF,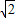 EC,
EC,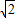 x,
x,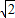 ,
,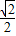 DE=2,
DE=2,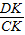 =
= =
= ,CD=
,CD=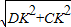 =2
=2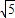 ,
, CD=
CD=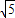 ,BC=5,
,BC=5,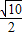 ,
, DK=1,CH=
DK=1,CH= CD=
CD=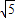 ,
,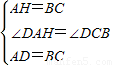 ,
,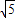 ,CA=
,CA=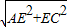 =2
=2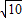 ,
,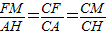 =
= ,
, ,CM=
,CM=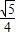 ,MH=
,MH=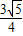 ,
, ,
,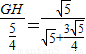 ,
, .
.

 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com