
| A. | 直角三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
分析 由方程有两个相等的实数根以及该方程为一元二次方程,结合根的判别式即可得出关于a、b、c的方程组,解方程组即可得出a2=b2+c2,由此即可得出结论.
解答 解:∵关于x的一元二次方程(a-c)x2-2bx+(a+c)=0有两个相等的实数根,
∴$\left\{\begin{array}{l}{△=0}\\{a-c≠0}\end{array}\right.$,即$\left\{\begin{array}{l}{(-2b)^{2}-4(a-c)(a+c)=0}\\{a≠c}\end{array}\right.$,
解得:a2=b2+c2且a≠c.
又∵a、b、c是△ABC的三边长,
∴△ABC为直角三角形.
故选A.
点评 本题考查了根的判别式,解题的关键是求出a2=b2+c2.本题属于基础题,难度不大,解决该题型题目时,根据根的个数结合根的判别式得出方程(不等式或不等式组)是关键.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:选择题
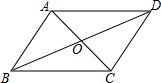 如图,平行四边形ABCD的对角线交于点O,且AB=6,△OCD的周长为19,则?ABCD的两条对角线的和是( )
如图,平行四边形ABCD的对角线交于点O,且AB=6,△OCD的周长为19,则?ABCD的两条对角线的和是( )| A. | 13 | B. | 25 | C. | 26 | D. | 38 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 购买一张福利彩票,中特等奖 | |
| B. | 在一个标准大气压下,加热水到100℃,沸腾 | |
| C. | 任意三角形的内角和为180° | |
| D. | 在一个仅装着白球和黑球的袋中摸出红球 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≤2 | B. | x<4 | C. | 2≤x<4 | D. | x≥2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com