
ФД¶БАнҪвЈә
јЖЛгЈә(Јӯ7![]() )Јӯ(Јӯ18
)Јӯ(Јӯ18![]() )Ј«(Јӯ5
)Ј«(Јӯ5![]() )Јӯ6
)Јӯ6![]() Ј®
Ј®
ҪвОцЈәТтОӘЈӯ7![]() ЈҪ(Јӯ7)Ј«(Јӯ
ЈҪ(Јӯ7)Ј«(Јӯ![]() )Ј¬
)Ј¬
18![]() ЈҪ18Ј«
ЈҪ18Ј«![]() Ј¬
Ј¬
Јӯ5![]() ЈҪ(Јӯ7)Ј«(Јӯ
ЈҪ(Јӯ7)Ј«(Јӯ![]() )Ј¬
)Ј¬
Јӯ6![]() ЈҪ(Јӯ5)Ј«(Јӯ
ЈҪ(Јӯ5)Ј«(Јӯ![]() )Ј®
)Ј®
ФӯКҪЈҪ(Јӯ7![]() )Ј«18
)Ј«18![]() Ј«(Јӯ5
Ј«(Јӯ5![]() )Јӯ6
)Јӯ6![]()
ЈҪ[(Јӯ7)Ј«(Јӯ![]() ]Ј«(18Ј«
]Ј«(18Ј«![]() )Ј«[(Јӯ5)Ј«(Јӯ
)Ј«[(Јӯ5)Ј«(Јӯ![]() )]Ј«[(Јӯ6)Ј«(Јӯ
)]Ј«[(Јӯ6)Ј«(Јӯ![]() )]
)]
ЈҪ[(Јӯ7)Ј«18Ј«(Јӯ5)Ј«(Јӯ6)]Ј«[(Јӯ![]() )Ј«
)Ј«![]() Ј«(Јӯ
Ј«(Јӯ![]() )Ј«(Јӯ
)Ј«(Јӯ![]() )]
)]
ЈҪ0Ј«(Јӯ1![]() )
)
ЈҪЈӯ1![]() Ј®
Ј®
ЙПГжХвЦЦјЖЛг·Ҫ·ЁҪРІрПо·ЁЈ¬ЗлДг·ВХХЙПГжөД·Ҫ·ЁјЖЛгЈә(Јӯ187![]() )Јӯ643
)Јӯ643![]() Ј«(Јӯ62
Ј«(Јӯ62![]() )Јӯ(Јӯ92
)Јӯ(Јӯ92![]() )Ј®
)Ј®
 УЕЙъАЦФ°ПөБРҙр°ё
УЕЙъАЦФ°ПөБРҙр°ё РВұаРЎС§өҘФӘЧФІвМвПөБРҙр°ё
РВұаРЎС§өҘФӘЧФІвМвПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәФД¶БАнҪв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәФД¶БАнҪв
| 5 |
| 6 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
| 5 |
| 6 |
| 5 |
| 6 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 6 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
| 5 |
| 6 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 5 |
| 6 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәФД¶БАнҪв
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 7 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 7 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
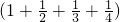 ЎБ
ЎБ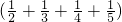 -
-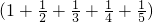 ЎБ
ЎБ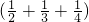 КұЈ¬Иф°С
КұЈ¬Иф°С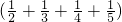 УлЈЁ
УлЈЁ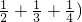 ·ЦұрёчҝҙЧЕТ»ёцХыМеЈ¬ФЩАыУГ·ЦЕдВЙҪшРРФЛЛгЈ¬ҝЙТФҙуҙујт»ҜДС¶ИЈ®№эіМИзПВЈә
·ЦұрёчҝҙЧЕТ»ёцХыМеЈ¬ФЩАыУГ·ЦЕдВЙҪшРРФЛЛгЈ¬ҝЙТФҙуҙујт»ҜДС¶ИЈ®№эіМИзПВЈә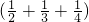 ОӘAЈ¬
ОӘAЈ¬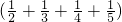 ОӘBЈ¬
ОӘBЈ¬ Ј®ЗлУГЙПГж·Ҫ·ЁјЖЛгЈә
Ј®ЗлУГЙПГж·Ҫ·ЁјЖЛгЈә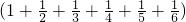
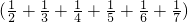
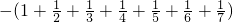
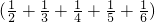
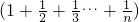
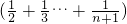

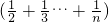 Ј®
Ј®Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com