

| 2 |
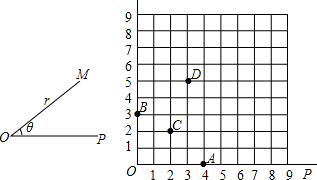
 解:(1)B点的坐标为(0,3);C点坐标为(2,2);
解:(1)B点的坐标为(0,3);C点坐标为(2,2);| 2 |
| 2 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:


查看答案和解析>>
科目:初中数学 来源:学习周报 数学 华师大八年级版 2009-2010学年 第9期 总第165期 华师大版 题型:022
我们知道,在直角三角形中,已知任意两条边的长度便能求出第三条边的长度.如果在直角三角形中,已知一条边的长度及另外两条边之间的关系时,我们就需要设未知数,并根据题意列出方程来解决问题.例如,已知在Rt△ABC中,∠C=90°,AC=![]() ,BC边长为AB边长的一半,则BC=________,AB=________
,BC边长为AB边长的一半,则BC=________,AB=________
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com