

分析 发现(1)只要证明△ACA′是等边三角形即可解决问题.
(2)分别证明S△ACB′=S△ACA′,S△A′BC=S△ACA′,即可.
拓展先证明∠ACB=∠CAA′=∠CA′A=α,在△CAA′利用三角形内角和定理即可解决.
探究(1)先证明∠BAC=30°,再在等腰三角形△ACC′根据内角和定理即可解决.
(2)在等腰三角形△ACC′根据内角和定理即可解决.
解答 发现:
解:(1)如图①中,在RT△ABC中,∵∠ACB=90°,∠B=30°,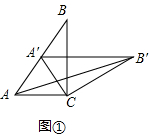
∴∠CAB=60°,
∵CA=CA′,
∴△ACA′是等边三角形,
∴∠ACA′=∠CA′B′=60°,
∴A′B′∥AC,
故答为平行.
(2)∵A′B′∥AC,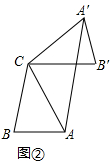 ∴S△ACB′=S△ACA′,
∴S△ACB′=S△ACA′,
∵△ACA′是等边三角形,
∴AA′=AC,
∵AB=2AC,
∴AA′=A′B,
∴S△A′BC=S△ACA′,
∴S△A′BC=S△ACB,即S1=S2.
故答案为相等.
拓展:如图②中,∵CA=CA′,AA′∥BC,
∴∠ACB=∠CAA′=∠CA′A=α,
∴β+2α=180°,
∴β=180°-2α.(0<α<90°)
故答案为180°-2α.
探究:解:(1)如图③中,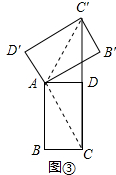 连接AC′、AC,
连接AC′、AC,
∵BC=1.AB=$\sqrt{3}$,∠B=90°
∴tan∠BAC=$\frac{BC}{AB}$=$\frac{\sqrt{3}}{3}$,
∴∠BAC=30°,
∵AB∥CC′,
∴∠ACC′=∠BAC=30°,
∵AC=AC′,
∴∠ACC′=∠AC′C=30°,
∴∠CAC′=180°-∠ACC′-∠AC′C=120°,
∴旋转角=120°
故答案为120°.
(2)由(1)可知∠CAC′=180°-∠ACC′-∠AC′C=180°-2α,
∴β=180°-2α,
∴α=90°-$\frac{1}{2}$β.
故答案为α=90°-$\frac{1}{2}$β.
点评 本题考查四边形综合题,锐角三角函数,等边三角形的判定和性质、等腰三角形的性质,三角形内角和定理等知识,解题的关键是灵活运用这些知识解决问题,属于中考常考题型.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:填空题
 如图,在四边形ABCD中,∠ABC=30°,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,若AB=3,BC=4,则BD=5(提示:可连接BE)
如图,在四边形ABCD中,∠ABC=30°,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,若AB=3,BC=4,则BD=5(提示:可连接BE)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>0,b>0 | B. | k<0,b>0 | C. | k<0,b<0 | D. | k<0,b>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
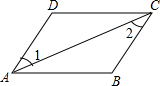 如图,在四边形ABCD中,若∠1=∠2,则AD∥BC,理由是( )
如图,在四边形ABCD中,若∠1=∠2,则AD∥BC,理由是( )| A. | 两直线平行,内错角相等 | B. | 两直线平行,同位角相等 | ||
| C. | 内错角相等,两直线平行 | D. | 同位角相等,两直线平行 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
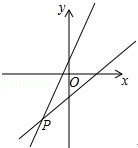 一次函数y=3x+b和y=ax-3的图象如图所示,其交点为P(-2,-5),则不等式3x+b>ax-3的解集在数轴上表示正确的是( )
一次函数y=3x+b和y=ax-3的图象如图所示,其交点为P(-2,-5),则不等式3x+b>ax-3的解集在数轴上表示正确的是( )| A. | 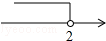 | B. |  | C. | 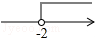 | D. | 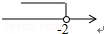 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )| A. | PA=PB | B. | PO平分∠APB | C. | AB垂直平分OP | D. | ∠OBA=∠OAB |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
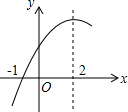 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:
二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com