
 如图是由边长为2的六个等边三角形组成的正六边形,建立适当的直角坐标系,求各顶点的坐标.
如图是由边长为2的六个等边三角形组成的正六边形,建立适当的直角坐标系,求各顶点的坐标. 分析 根据题意可以做出合适的平面直角坐标系,然后写出相应的各个顶点的坐标即可解答本题.
解答 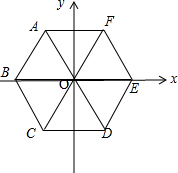 解:以正六边形的中心为坐标原点,建立平面直角坐标系如右图所示,
解:以正六边形的中心为坐标原点,建立平面直角坐标系如右图所示,
∵右图是由边长为2的六个等边三角形组成的正六边形,
∴OA=AB=OB=2,∠AOB=60°,
∴点A的横坐标是:-2×cos60°=-1,纵坐标是:2×sin60°=$\sqrt{3}$,
即点A的坐标是:(-1,$\sqrt{3}$),
同理可得,点B的坐标为(-2,0),点C的坐标为(-1,-$\sqrt{3}$),点D的坐标为(1,-$\sqrt{3}$),点E的坐标为(2,0),点F的坐标为(1,$\sqrt{3}$).
点评 本题考查坐标与图形的性质,解题的关键是明确题意,建立合适的平面直角坐标系,利用数形结合的思想解答.


科目:初中数学 来源: 题型:解答题
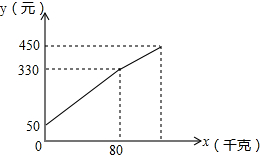 李大爷按每千克2.1元批发了一批蜜橘到镇上出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降低出售.售出蜜橘千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:
李大爷按每千克2.1元批发了一批蜜橘到镇上出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降低出售.售出蜜橘千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2-x}{1-x}$ | B. | x+1 | C. | x-1 | D. | $\frac{1}{2-x}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com