
已知:如图,在梯形ABCD中,AD∥BC,∠DCB=90°,E是AD的中点,点P是BC边上的动点(不与点B重合),EP与BD相交于点O.
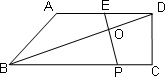
(1)当P点在BC边上运动时,求证:△BOP∽△DOE;
(2)设(1)中的相似比为k,若AD∶BC=2∶3.请探究:当k为下列三种情况时,四边形ABPE是什么四边形?①当k=1时,是________;②当k=2时,是________;③当k=3时,是________.并证明k=2时的结论.
|
(1)证明:∵AD∥BC ∴∠OBP=∠ODE 1 分在 △BOP和△DOE中∠OBP=∠ODE ∠BOP=∠DOE 2 分∴△BOP∽△DOE(有两个角对应相等的两三角形相似) 3 分
(2)①平行四边形 4 分②直角梯形 5 分③等腰梯形 6 分 证明:∵k=2时, ∴BP=2DE=AD 又 ∵AD∶BC=2∶3 BC= PC=BC-BP= ED∥PC,∴四边形PCDE是平行四边形 ∵∠DCB=90° ∴四边形PCDE是矩形 7 分∴∠EPB=90° 8 分又∵在直角梯形ABCD中 AD∥BC,AB与DC不平行 ∴AE∥BP,AB与EP不平行 四边形ABPE是直角梯形 9 分
(本题其它证法参照此标准给分) |


科目:初中数学 来源: 题型:
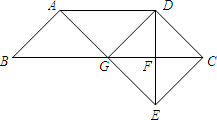 (2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G.
(2013•闵行区二模)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2AD.DE⊥BC,垂足为点F,且F是DE的中点,联结AE,交边BC于点G.| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.
已知:如图,在梯形ABCD中,AD∥BC,CD=10cm,∠B=45度,∠C=30度,AD=5cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com