
| 2 |
| 3 |
| 3 |
| 35 |
| 24 |

| 2 |
| 3 |
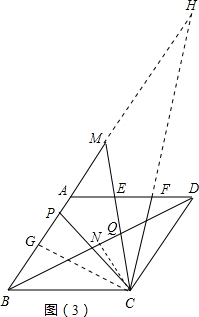
 (1)证明:连接AC,在菱形ABCD中,∵∠BAD=90°,
(1)证明:连接AC,在菱形ABCD中,∵∠BAD=90°,| AP |
| DQ |
| AC |
| CD |
| ||
| 1 |
| 2 |
| 2 |
| 2 |

| 3 |
| 3 |
| 3 |
| 5 |
| 2 |
5
| ||
| 2 |
| MC2-CG2 |
| 11 |
| 2 |
| 15 |
| 8 |
| 10 |
| 3 |
| 35 |
| 24 |
| 35 |
| 24 |
| 5 |
| 2 |
5
| ||
| 2 |
| 3 |
| 5 |
| 13 |
25
| ||
| 13 |
| 3 |
| 55 |
| 13 |


科目:初中数学 来源: 题型:
 (2012•南岗区一模)如图,边长为1的正方形ABCD绕点A旋转得到正方形AB1ClD1,若AB1落在对角线AC上,连接A0,则∠AOB1等于( )
(2012•南岗区一模)如图,边长为1的正方形ABCD绕点A旋转得到正方形AB1ClD1,若AB1落在对角线AC上,连接A0,则∠AOB1等于( )查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•南岗区一模)王大爷要围成一个如图所示的矩形ABCD花圃.花圃的一边利用20米长的墙,另三边用总长为36米的篱笆恰好围成.设A8边的长为x米,BC的长为y米,且BC>AB.
(2012•南岗区一模)王大爷要围成一个如图所示的矩形ABCD花圃.花圃的一边利用20米长的墙,另三边用总长为36米的篱笆恰好围成.设A8边的长为x米,BC的长为y米,且BC>AB.| b |
| 2a |
| 4ac-b2 |
| 4a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com