
已知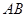 是半圆
是半圆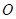 的直径, 点
的直径, 点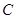 在
在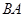 的延长线上运动(点
的延长线上运动(点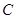 与点
与点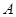 不重合), 以
不重合), 以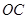 为直径的半圆
为直径的半圆 与半圆
与半圆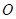 交于点
交于点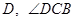 的平分线与半圆
的平分线与半圆 交于点
交于点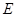 .
.
如图甲, 求证: 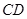 是半圆
是半圆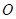 的切线;
的切线;
如图乙, 作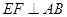 于点
于点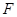 , 猜想
, 猜想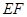 与已有的哪条线段的一半相等, 并加以证明;
与已有的哪条线段的一半相等, 并加以证明;
如图丙, 在上述条件下, 过点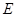 作
作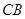 的平行线交
的平行线交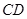 于点
于点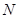 , 当
, 当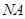 与半圆
与半圆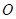 相切时, 求
相切时, 求
甲 乙  的正切值.
的正切值.
角度转换;三角形全等的变换;3
解析试题分析:(1) 如图甲, 连接 , 则
, 则 为半圆
为半圆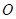 的半径, 而
的半径, 而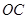 为半圆
为半圆 的直径, 所以
的直径, 所以 ,
,
即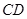 是半圆
是半圆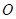 的切线;
的切线;
(2) 猜想:  .
.
证1: 如图乙, 以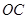 为直径作⊙
为直径作⊙ , 延长
, 延长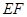 交⊙
交⊙ 于点
于点 ,连接
,连接 ,
,
∵ , ∴
, ∴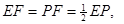 ∵
∵ 平分
平分 , ∴
, ∴ ,
,
∴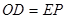 , ∴
, ∴ ;
;
甲 乙 丙 丁
证2: 如图丙, 连接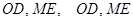 相交于点
相交于点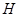 . ∵
. ∵ 平分
平分 , ∴
, ∴ ,
,
∴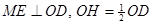 , ∴可证
, ∴可证 , ∴
, ∴ ;
;
(3) 如图丁, 延长 交
交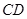 于点
于点 , 设
, 设 , 则
, 则 ,
,
∵四边形 是矩形, ∴
是矩形, ∴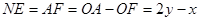 , 同(2)证法
, 同(2)证法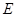 是
是 中点,
中点,
∴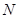 是
是 中点, ∴
中点, ∴ ,
,
可证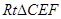 ∽
∽ , ∴
, ∴ , 即
, 即 , 解得
, 解得 或
或 .
.
当 时, 点
时, 点 与点
与点 重合, 舍去; 当
重合, 舍去; 当 时,
时,  .
.
考点:全等三角形的性质和判定
点评:解答本题的关键是熟练掌握判定两个三角形全等的一般方法:SSS、SAS、ASA、AAS、HL,注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


科目:初中数学 来源:2011年河南省新乡市三十中中考模拟数学卷 题型:解答题
(10分)如图所示,已知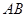 是半圆
是半圆 的直径,弦
的直径,弦 ,
,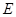 是
是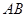 延长线上一点,
延长线上一点,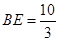 .判断直线
.判断直线 与半圆
与半圆 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.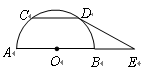
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江省杭州市九年级中考二模(5月)数学试卷(解析版) 题型:解答题
已知 是半圆
是半圆 的直径, 点
的直径, 点 在
在 的延长线上运动(点
的延长线上运动(点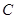 与点
与点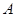 不重合), 以
不重合), 以 为直径的半圆
为直径的半圆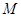 与半圆
与半圆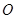 交于点
交于点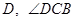 的平分线与半圆
的平分线与半圆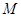 交于点
交于点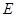 .
.
如图甲, 求证: 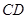 是半圆
是半圆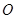 的切线;
的切线;
如图乙, 作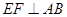 于点
于点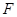 , 猜想
, 猜想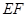 与已有的哪条线段的一半相等, 并加以证明;
与已有的哪条线段的一半相等, 并加以证明;
如图丙, 在上述条件下, 过点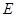 作
作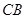 的平行线交
的平行线交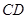 于点
于点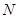 , 当
, 当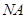 与半圆
与半圆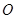 相切时, 求
相切时, 求

甲 乙
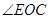 的正切值.
的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com