
(阅读下面的题目及分析过程,并按要求进行证明.
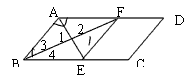
已知:如图,E是BC的中点,点A在DE上,且∠BAE=∠CDE.

求证:AB=CD.
分析:证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等.因此,要证AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.
现给出如下三种添加辅助线的方法,请任意选择其中一种,对原题进行证明.

【解析】
试题分析:方法一:作BF⊥DE于点F,CG⊥DE于点G,∴∠F=∠CGE=90°.又∵∠BEF=∠CEG,BE=CE,∴△BFE≌△CGE.∴BF=CG.在△ABF和△DCG中,∵∠F=∠DGC=90°,∠BAE=∠CDE,BF=CG,∴△ABF≌△DCG.∴AB=CD.
方法二:作CF∥AB,交DE的延长线于点F,∴∠F=∠BAE.又∵∠ABE=∠D,∴∠F=∠D.∴CF=CD.
∵∠F=∠BAE,∠AEB=∠FEC,BE=CE,∴△ABE≌△FCE.∴AB=CF.∴AB=CD.
方法三:延长DE至点F,使EF=DE,又∵BE=CE,∠BEF=∠CED,∴△BEF≌△CED.∴BF=CD,∠D=∠F.又∵∠BAE=∠D,∴∠BAE=∠F.∴AB=BF.∴AB=CD.
考点:1.全等三角形的判定与性质;2.阅读理解.


科目:初中数学 来源:同步题 题型:解答题
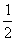 ∠BAF,∠3=∠4=
∠BAF,∠3=∠4=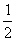 ∠ABE,
∠ABE, 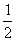 (∠BAF+∠ABE)=90。
(∠BAF+∠ABE)=90。查看答案和解析>>
科目:初中数学 来源:专项题 题型:解答题
 ∠BAF,∠3=∠4=
∠BAF,∠3=∠4= ∠ABE
∠ABE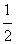 (∠BAF+∠ABE)=
(∠BAF+∠ABE)= ×180°=90°
×180°=90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com