
| ||
| 2 |

| 13 |
| 3 |
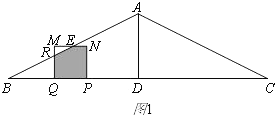
| BP |
| BD |
| NP |
| AD |
| BP |
| 4 |
| 1 |
| 2 |
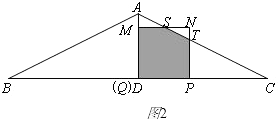
| NP |
| AD |
| CP |
| CD |
| a |
| 2 |
| 4-a |
| 4 |
| 4 |
| 3 |
| 16 |
| 3 |
| 13 |
| 3 |
| 13 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 13 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 5 |
| 4 |
| 27 |
| 2 |
| 133 |
| 4 |
|
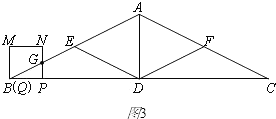
| BP |
| BD |
| PG |
| AD |
| 1 |
| 4 |
| PG |
| 2 |
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |


科目:初中数学 来源: 题型:
 已知关于x的一元二次方程x2-(5m+1)x+4m2+m=0.
已知关于x的一元二次方程x2-(5m+1)x+4m2+m=0.查看答案和解析>>
科目:初中数学 来源: 题型:
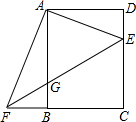 如图,在矩形ABCD中,AB=8,BC=6,点E是边CD上一个动点(点E与点C、点D不重合),连接AE,作AF⊥AE,交直线CB于点F,连接EF,交边AB于点G.设DE=x,BF=y.
如图,在矩形ABCD中,AB=8,BC=6,点E是边CD上一个动点(点E与点C、点D不重合),连接AE,作AF⊥AE,交直线CB于点F,连接EF,交边AB于点G.设DE=x,BF=y.查看答案和解析>>
科目:初中数学 来源: 题型:
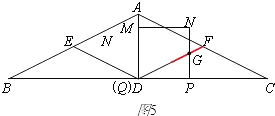
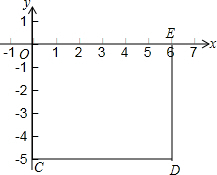
 如图,某景点在山顶C处,以前人们从A处出发沿着坡比为1:2的缓坡AB爬行200米到达B处,再由B处沿着坡角为60°的陡坡BC蹬阶180米到达C处,整个路程比较危险.后来管理部门在A、C之间架设了索道,已知索道AC与水平面AE的夹角为45°,求索道AC的长.
如图,某景点在山顶C处,以前人们从A处出发沿着坡比为1:2的缓坡AB爬行200米到达B处,再由B处沿着坡角为60°的陡坡BC蹬阶180米到达C处,整个路程比较危险.后来管理部门在A、C之间架设了索道,已知索道AC与水平面AE的夹角为45°,求索道AC的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com