
分析 (1)根据每件服装毛利润=销售价-进货价,由此即可求出每天销售这种服装的毛利润y(元)与每件销售价x(元)之间的函数表达式.
(2)利用配方法求出二次函数的最大值即可.
(3)列出一元二次不等式,解不等式,结合题意确定销售单价即可.
解答 解:(1)由题意,销售利润y(元)与每件的销售价x(元)之间的函数关系为
y=(x-42)(-3x+204),
即y=-3x2+330x-8568.
故商场卖这种服装每天的销售利润y(元)与每件的销售价x(元)之间的函数关系式为y=-3x2+330x-8568;
(2)配方,得y=-3(x-55)2+507.
故当每件的销售价为55元时,可取得最大利润,每天最大销售利润为507元.
(3)由题意-3(x-55)2+507≥480,
解得52≤x≤58,
为了尽可能地增加销量,减少库存,
又销量t=204-3x,
t随着x的增加而减小,
所以销售价格应为52元时销量最大.
点评 本题主要考查运用待定系数法求一次函数的解析式及二次函数的应用,根据利润=(售价-成本)×销售量列出函数关系式,另外要熟练掌握二次函数求最值的方法.要注意应该在自变量的取值范围内求最大值(或最小值),也就是说二次函数的最值不一定在在x=-$\frac{b}{2a}$时取得.此类题是近年中考中的热点问题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:解答题
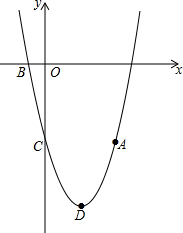 如图,抛物线y=ax2+bx-5(a≠0)经过点A(4,-5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.
如图,抛物线y=ax2+bx-5(a≠0)经过点A(4,-5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
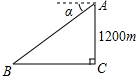 如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=43°,求飞机A与指挥台B的距离(结果取整数)
如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=43°,求飞机A与指挥台B的距离(结果取整数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com