
如图,⊙O是△ACD的外接圆,AB是直径,过点D作直线DE∥AB,过点B作直线BE∥AD,两直线交于点E,如果∠ACD=45°,⊙O的半径是4cm
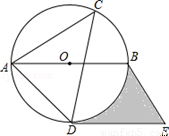
(1)请判断DE与⊙O的位置关系,并说明理由;
(2)求图中阴影部分的面积(结果用π表示).
(1)相切,理由见解析;(2)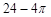 .
.
【解析】
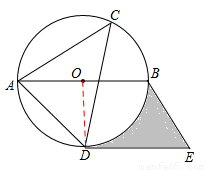
试题分析:(1)连接OD,根据圆周角定理得∠ABD=∠ACD=45°,∠ADB=90°,可判断△ADB为等腰直角三角形,所以OD⊥AB,而DE∥AB,则有OD⊥DE,然后根据切线的判定定理得到DE为⊙O的切线;(2)由BE∥AD,DE∥AB得到四边形ABED为平行四边形,则DE=AB=8cm,然后根据梯形的面积公式和扇形的面积公式,利用S阴影部分=S梯形BODE﹣S扇形OBD求得图中阴影部分的面积.
试题解析:(1)DE与⊙O相切. 理由如下:
如图,连接OD,则∠ABD=∠ACD=45°.
∵AB是直径,∴∠ADB=90°. ∴△ADB为等腰直角三角形.
∵点O为AB的中点,∴OD⊥AB.
∵DE∥AB,∴OD⊥DE. ∴DE为⊙O的切线.
(2)∵BE∥AD,DE∥AB,∴四边形ABED为平行四边形.
∴DE=AB=8cm.
∴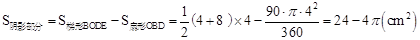 .
.
考点:1.圆周角定理;2.等腰直角三角形的判定和性质;3.平行的性质;4.切线的判定;5.平行四边形的判定和性质;6.扇形面积的计算;7.转换思想的应用.


科目:初中数学 来源: 题型:
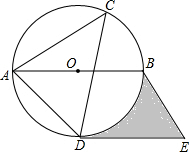 (2013•本溪)如图,⊙O是△ACD的外接圆,AB是直径,过点D作直线DE∥AB,过点B作直线BE∥AD,两直线交于点E,如果∠ACD=45°,⊙O的半径是4cm
(2013•本溪)如图,⊙O是△ACD的外接圆,AB是直径,过点D作直线DE∥AB,过点B作直线BE∥AD,两直线交于点E,如果∠ACD=45°,⊙O的半径是4cm查看答案和解析>>
科目:初中数学 来源:2013-2014学年福建莆田青璜中学九年级下学期期初考试数学试卷(解析版) 题型:解答题
如图,⊙O是△ACD的外接圆,AB是直径,过点D作直线DE∥AB,过点B作直线BE∥AD,两直线交于点E,∠ACD=45°,⊙O的半径是4cm.
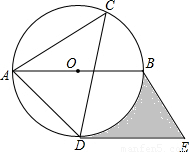
(1)请判断DE与⊙O的位置关系,并说明理由;
(2)求图中阴影部分的面积(结果用π表示).
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江西省九年级3月月考数学试卷(解析版) 题型:解答题
如图,⊙O是△ACD的外接圆,AB是直径,过点D作直线DE∥AB,过点B作直线BE∥AD,两直线交于点E,如果∠ACD=45°,⊙O的半径是4cm
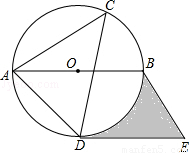
(1)请判断DE与⊙O的位置关系,并说明理由;
(2)求图中阴影部分的面积(结果用π表示).
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(辽宁本溪卷)数学(解析版) 题型:解答题
如图,⊙O是△ACD的外接圆,AB是直径,过点D作直线DE∥AB,过点B作直线BE∥AD,两直线交于点E,如果∠ACD=45°,⊙O的半径是4cm
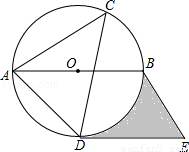
(1)请判断DE与⊙O的位置关系,并说明理由;
(2)求图中阴影部分的面积(结果用π表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com