
如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,ΔPEF、ΔPDC、ΔPAB的面积分别为S、S1、S2..若S=2,则S1+S2= .

8.
【解析】
试题分析:过P作PQ平行于DC,由DC与AB平行,得到PQ平行于AB,可得出四边形PQCD与ABQP都为平行四边形,进而确定出△PDC与△PCQ面积相等,△PQB与△ABP面积相等,再由EF为△BPC的中位线,利用中位线定理得到EF为BC的一半,且EF平行于BC,得出△PEF与△PBC相似,相似比为1:2,面积之比为1:4,求出△PBC的面积,而△PBC面积=△CPQ面积+△PBQ面积,即为△PDC面积+△PAB面积,即为平行四边形面积的一半,即可求出所求的面积.
试题解析:过P作PQ∥DC交BC于点Q,由DC∥AB,得到PQ∥AB,
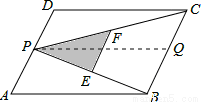
∴四边形PQCD与四边形APQB都为平行四边形,
∴△PDC≌△CQP,△ABP≌△QPB,
∴S△PDC=S△CQP,S△ABP=S△QPB,
∵EF为△PCB的中位线,
∴EF∥BC,EF=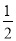 BC,
BC,
∴△PEF∽△PBC,且相似比为1:2,
∴S△PEF:S△PBC=1:4,S△PEF=2,
∴S△PBC=S△CQP+S△QPB=S△PDC+S△ABP=S1+S2=8.
考点:1.平行四边形的性质;2.相似三角形的判定与性质.


科目:初中数学 来源:2014-2015学年江苏省扬州市邗江区八年级上学期期中测试数学试卷(解析版) 题型:选择题
下列说法中,正确的是( )
A.两个全等三角形一定关于某直线对称
B.等边三角形的高、中线、角平分线都是它的对称轴
C.两个图形关于某直线对称,则这两个图形一定分别位于这条直线的两侧
D.关于某直线对称的两个图形是全等形
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,在菱形ABCD中,AC、BD交于点O,AC=12cm,BD=16cm。动点P在线段AB上,由B向A运动,速度为1cm/s,动点Q在线段OD上,由D向O运动,速度为1cm/s。过点Q作直线EF┴BD交AD于E,交CD于F,连接PF,设运动时间为t(0<t<8)。问

(1)何时四边形APFD为平行四边形?求出相应t的值;
(2)设四边形APFE面积为ycm2,求y与t的函数关系式;.
(3)是否存在某一时刻t,使S四边形APFE:S菱形ABCD=17:40?若存在,求出相应t的值,并求出,P、E两点间的距离,若不存在,说明理由。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级上学期期中考试数学试卷(解析版) 题型:解答题
已知四边形ABCD顶点都在4×4的正方形网格格点上,如图所示,

(1)请画出四边形ABCD的外接圆,并标明圆心M的位置;
(2)这个圆中弦BC所对的圆周角的度数是 。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,菱形ABCD中,点M,N在AC上,ME⊥AD, NF⊥AB.若NF = NM = 2,ME = 3,则AN 为( )

A.3 B.4 C.5 D.6
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省启东市八年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.

(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com