
已知:等边![]() 的边长为
的边长为![]() .
.
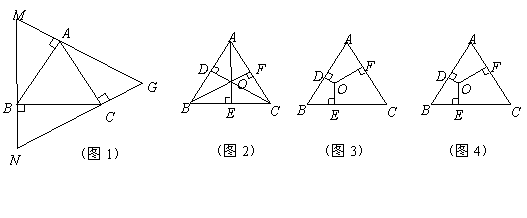
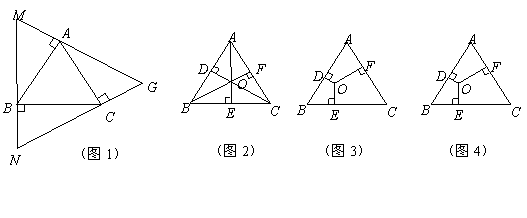
探究(1):如图1,过等边![]() 的顶点
的顶点![]() 依次作
依次作![]() 的垂线围成
的垂线围成![]() 求证:
求证:![]() 是等边三角形且
是等边三角形且![]() ;
;
探究(2):在等边![]() 内取一点
内取一点![]() ,过点
,过点![]() 分别作
分别作![]() 垂足分别为点
垂足分别为点![]()
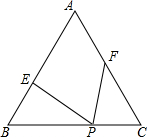
①如图2,若点![]() 是
是![]() 的重心,我们可利用三角形面积公式及等边三角形性质得到两个正确结论(不必证明):结论1.
的重心,我们可利用三角形面积公式及等边三角形性质得到两个正确结论(不必证明):结论1.![]() ;结论2.
;结论2.![]() ;
;
②如图3,若点![]() 是等边
是等边![]() 内任意一点,则上述结论
内任意一点,则上述结论![]() 是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.
是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.
 |
科目:初中数学 来源: 题型:
 (2013•海门市一模)已知,等边△ABC边长为6,P为BC边上一点,且BP=4,点E、F分别在边AB、AC上,且∠EPF=60°,设BE=x,CF=y.
(2013•海门市一模)已知,等边△ABC边长为6,P为BC边上一点,且BP=4,点E、F分别在边AB、AC上,且∠EPF=60°,设BE=x,CF=y.| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 ,点
,点 在
在 正半轴上,且
正半轴上,且 .动点
.动点 在线段
在线段 上从点
上从点 向点
向点 以每秒
以每秒 个单位的速度运动,设运动时间为秒.点M、N在
个单位的速度运动,设运动时间为秒.点M、N在 轴上,且
轴上,且 是等边三角形.
是等边三角形. 的边长(用的代数式表示),并求出当等边
的边长(用的代数式表示),并求出当等边 的顶点
的顶点 运动到与原点
运动到与原点 重合时的值;
重合时的值; 的中点
的中点 ,以
,以 为边在
为边在 内部作如图2所示的矩形
内部作如图2所示的矩形 ,点
,点 在线段
在线段 上.设等边
上.设等边 和矩形
和矩形 重叠部分的面积为
重叠部分的面积为 ,请求出当
,请求出当 秒时,
秒时, 与的函数关系式,并求出
与的函数关系式,并求出 的最大值.
的最大值.



查看答案和解析>>
科目:初中数学 来源: 题型:
已知:等边![]() 的边长为
的边长为![]() .
.
探究(1):如图1,过等边![]() 的顶点
的顶点![]() 依次作
依次作![]() 的垂线围成
的垂线围成![]() 求证:
求证:![]() 是等边三角形且
是等边三角形且![]() ;
;
探究(2):在等边![]() 内取一点
内取一点![]() ,过点
,过点![]() 分别作
分别作![]() 垂足分别为点
垂足分别为点![]()
(2)如图2,若点![]() 是
是![]() 的重心,我们可利用三角形面积公式及等边三角形性质得到两个正确结论(不必证明):
的重心,我们可利用三角形面积公式及等边三角形性质得到两个正确结论(不必证明):
① 结论1.![]() ;
;
② 结论2.![]() ;
;
(3)如图3,若点![]() 是等边
是等边![]() 内任意一点,则上述结论
内任意一点,则上述结论![]() 是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.
是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:等边![]() 的边长为
的边长为![]() .
.
探究(1):如图1,过等边![]() 的顶点
的顶点![]() 依次作
依次作![]() 的垂线围成
的垂线围成![]() 求证:
求证:![]() 是等边三角形且
是等边三角形且![]() ;
;
探究(2):在等边![]() 内取一点
内取一点![]() ,过点
,过点![]() 分别作
分别作![]() 垂足分别为点
垂足分别为点![]()
①如图2,若点![]() 是
是![]() 的重心,我们可利用三角形面积公式及等边三角形性质得到两个正确结论(不必证明):结论1.
的重心,我们可利用三角形面积公式及等边三角形性质得到两个正确结论(不必证明):结论1.![]() ;结论2.
;结论2.![]() ;
;
②如图3,若点![]() 是等边
是等边![]() 内任意一点,则上述结论
内任意一点,则上述结论![]() 是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.
是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com