
如图,已知等边△ABC中,点D、E分别在边AB、BC上,把△BDE沿直线DE翻折,使点B落在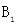 处,
处,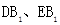 分别交边AC于M、H点,若∠ADM=50°,则∠EHC的度数为( ).
分别交边AC于M、H点,若∠ADM=50°,则∠EHC的度数为( ).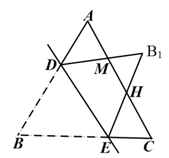
A.45°B.50°C.55°D.60°
 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:单选题
下列说法正确的是( ).
| A.三角形的重心是三角形三边垂直平分线的交点. |
| B.三角形的一条中位线与第三边上的中线互相平分. |
C.坡面的水平长度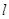 与铅垂高度 与铅垂高度 的比是坡比 的比是坡比 |
| D.相似三角形对应高的比等于相似比的平方. |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
夏季的一天,身高为1.6m的小玲想测量一下屋前大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,于是得出树的高度为( )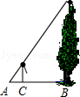
| A.8m | B.6.4m | C.4.8m | D.10m |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤当△PMN∽△AMP时,点P是AB的中点.其中正确的结论有( )
| A.2个 | B.3个 | C.4个 | D.5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
如图,在 ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,
ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F, ,则DE:EC=【 】
,则DE:EC=【 】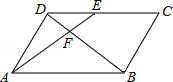
| A.2:5 | B.2:3 | C.3:5 | D.3:2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com