
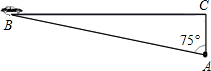
 超速行驶是引发交通事故的主要原因之一.上周末,四位同学尝试用自己所学的知识检测车速.如图,观测点设在A处,离迎宾大道(60千米/小时的限制速度)的距离(AC)为30米.这时,一辆小轿车由西向东匀速行驶,测得此车从B处行驶到C处所用的时间为8秒,∠BAC=75°.(计算时距离精确到1米,参考数据:sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.732,
超速行驶是引发交通事故的主要原因之一.上周末,四位同学尝试用自己所学的知识检测车速.如图,观测点设在A处,离迎宾大道(60千米/小时的限制速度)的距离(AC)为30米.这时,一辆小轿车由西向东匀速行驶,测得此车从B处行驶到C处所用的时间为8秒,∠BAC=75°.(计算时距离精确到1米,参考数据:sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.732,| 3 |
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,AB∥CD∥x轴,BC∥DE∥y轴,且AB=CD=4cm,OA=5cm,DE=2cm,动点P从点A出发,沿A→B→C路线运动到点C停止;动点Q从点O出发,沿O→E→D→C路线运动到点C停止;若P、Q两点同时出发,且点P的运动速度为1cm/s,点Q的运动速度为2cm/s.
如图,在平面直角坐标系中,AB∥CD∥x轴,BC∥DE∥y轴,且AB=CD=4cm,OA=5cm,DE=2cm,动点P从点A出发,沿A→B→C路线运动到点C停止;动点Q从点O出发,沿O→E→D→C路线运动到点C停止;若P、Q两点同时出发,且点P的运动速度为1cm/s,点Q的运动速度为2cm/s.| 11 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
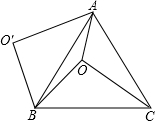 如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:
如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:| 3 |
| 9 |
| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
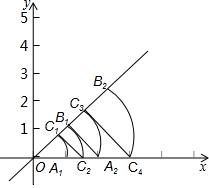 如图,已知直线l的表达式为y=x,点A1的坐标为(1,0),以O为圆心,OA1为半径画弧,与直线l交于点C1,记
如图,已知直线l的表达式为y=x,点A1的坐标为(1,0),以O为圆心,OA1为半径画弧,与直线l交于点C1,记 |
| A1C1 |
 |
| B1C2 |
 |
| A2C3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com