
如图,抛物线 与
与 轴相交于点
轴相交于点 (﹣1,0)、
(﹣1,0)、 (3,0),与
(3,0),与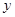 轴相交于点
轴相交于点 ,点
,点 为线段
为线段 上的动点(不与
上的动点(不与 、
、 重合),过点
重合),过点 垂直于
垂直于 轴的直线与抛物线及线段
轴的直线与抛物线及线段 分别交于点
分别交于点 、
、 ,点
,点 在
在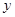 轴正半轴上,
轴正半轴上, =2,连接
=2,连接 、
、 .
.
(1)求抛物线的解析式;
(2)当四边形 是平行四边形时,求点
是平行四边形时,求点 的坐标;
的坐标;
(3)过点 的直线将(2)中的平行四边形
的直线将(2)中的平行四边形 分成面积相等的两部分,求这条直线的解析式.(不必说明平分平行四边形面积的理由)
分成面积相等的两部分,求这条直线的解析式.(不必说明平分平行四边形面积的理由)
(1)抛物线的解析式为: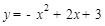 ;(2)
;(2) 点坐标为
点坐标为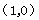 或
或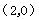 ;(3) ①当
;(3) ①当
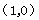 时,所求直线的解析式为:
时,所求直线的解析式为: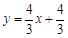 ;②当
;②当
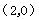 时,所求直线的解析式为:
时,所求直线的解析式为: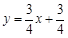 .
.
解析试题分析:
(1)将点 和点
和点 的坐标代入抛物线函数中,可求出未知量
的坐标代入抛物线函数中,可求出未知量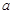 ,
,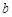 .则可求出该抛物线解析式;(2)由平行四边形的性质可知,
.则可求出该抛物线解析式;(2)由平行四边形的性质可知, ,用含未知量
,用含未知量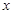 的代数式表示
的代数式表示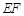 的长度。则可得点
的长度。则可得点 坐标 ;(3)平行四边形是中心对称图形,其对称中心为两条对角线的交点(或对角线的中点),过对称中心的直线平分平行四边形的面积,因此过点
坐标 ;(3)平行四边形是中心对称图形,其对称中心为两条对角线的交点(或对角线的中点),过对称中心的直线平分平行四边形的面积,因此过点 与
与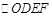 对称中心的直线平分
对称中心的直线平分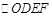 的面积.求得此直线,首先要求得
的面积.求得此直线,首先要求得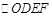 对称中心的坐标.则两点坐标可确定该直线.
对称中心的坐标.则两点坐标可确定该直线.
试题解析:
(1) 点
点
 、
、
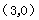 在抛物线
在抛物线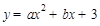 上,
上,
∴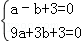 ,
,
解得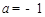 ,
,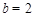 ,
,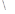 抛物线的解析式为:
抛物线的解析式为: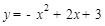 .
.
(2)在抛物线解析式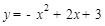 中,令
中,令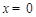 ,得
,得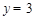 ,
,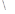

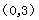 .
.
设直线BC的解析式为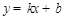 ,将
,将
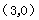 ,
,
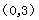 坐标代入得:
坐标代入得: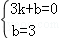 ,解得
,解得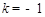 ,
,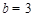 ,∴
,∴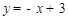 .
.
设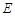 点坐标为
点坐标为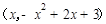 ,则
,则
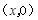 ,
,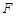
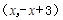 ,
,
∴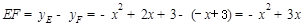
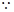 四边形
四边形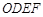 是平行四边形,
是平行四边形,
∴ ,
,
∴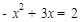 ,即
,即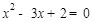 ,
,
解得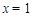 或
或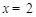 ,
,
∴ 点坐标为
点坐标为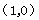 或
或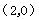 .
.
(3)平行四边形是中心对称图形,其对称中心为两条对角线的交点(或对角线的中点),过对称中心的直线平分平行四边形的面积,因此过点 与
与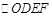 对称中心的直线平分
对称中心的直线平分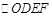 的面积.
的面积.
①当
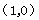 时,点
时,点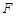 坐标为
坐标为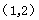 ,又
,又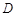
设对角线 的中点为
的中点为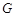 ,则
,则
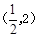 .
.
设直线 的解析式为
的解析式为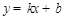 ,将
,将
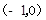 ,
,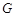
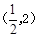 坐标代入得:
坐标代入得: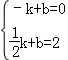 ,
,
解得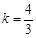 ,
, 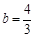 ,∴所求直线的解析式为:
,∴所求直线的解析式为: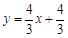


科目:初中数学 来源: 题型:解答题
如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).
(1)求直线BD和抛物线的解析式.
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知二次函数图象的顶点是(-1,2),且过点(0, ).
).
(1)求二次函数的表达式,并在图中画出它的图象;
(2)判断点(2, )是否在该二次函数图象上;并指出当
)是否在该二次函数图象上;并指出当 取何值时,
取何值时,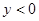 ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线 的顶点为Q,与
的顶点为Q,与 轴交于A(-1,0)、B(5, 0)两点,与
轴交于A(-1,0)、B(5, 0)两点,与 轴交于C点.
轴交于C点.
(1)直接写出抛物线的解析式及其顶点Q的坐标;
(2)在该抛物线的对称轴上求一点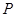 ,使得△
,使得△ 的周长最小.请在图中画出点
的周长最小.请在图中画出点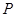 的位置,并求点
的位置,并求点 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线 与直线
与直线 交于点A 、B,与y轴交于点C.
交于点A 、B,与y轴交于点C.
(1)求点A、B的坐标;
(2)若点P是直线x=1上一点,是否存在△PAB是等腰三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,要设计一个矩形的花坛,花坛长60 m,宽40 m,有两条纵向甬道和一条横向甬道,横向甬道的两侧有两个半圆环形甬道,半圆环形甬道的内半圆的半径为10 m,横向甬道的宽度是其它各甬道宽度的2倍.设横向甬道的宽为2x m.(π的值取3)
(1)用含x的式子表示两个半圆环形甬道的面积之和;
(2)当所有甬道的面积之和比矩形面积的 多36 m2时,求x的值.
多36 m2时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知抛物线 的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)。
的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5)。
(1)求直线BC与抛物线的解析式;
(2)若点M是抛物线在x轴下方图象上的动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;
(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,设平行四边形CBPQ的面积为S1,△ABN的面积为S2,且S1=6S2,求点P的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com