
���� ��1���ɵڶ�����Ե�һ���������q��ֵ��ȷ������4��ɣ�
��2���������еĶ�������ܽ�õ�ͨ�ʽ���ɣ�
��3���ɹ���q��ڶ����ֵ�����һ���ֵ������ȷ������4���ֵ��
��� �⣺��1��q=$\frac{6}{3}$=2����4����24��
��2�������ܽ�ã�an=a1•qn-1��
��3���ߵȱ����еĹ���q=2���ڶ���Ϊ10��
��a1=$\frac{{a}_{2}}{q}$=5��a4=a1•q3=5��23=40��
�ʴ�Ϊ����1��2��24����2��a1•qn-1
���� ���⿼���˹����ͣ����ֵı仯�࣬Ū�����еĹ����ǽⱾ��Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢ܢ� | B�� | �ۢܢ� | C�� | �ܢݢ� | D�� | �ڢݢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-2y-x����x+2y�� | B�� | ��x-2y����-x-2y�� | C�� | ��x-2y����2y+x�� | D�� | ��2y-x����-x-2y�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 42������ƽ����Ϊ4 | B�� | $\sqrt{4}$������ƽ����Ϊ$\sqrt{2}$ | ||
| C�� | $\sqrt{{3}^{2}}$������ƽ������$\sqrt{3}$ | D�� | $\sqrt{81}$������ƽ������9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ����Ϣ��������˵��������������ǰ�����ٶ�С���ҵ��ٶȣ��ڳ�����1Сʱ�������г̾�Ϊ10km���۳�����1.5Сʱ�����г̱��Ҷ�3km���ܼױ����ȵ����յ㣮������ȷ���У�������
����Ϣ��������˵��������������ǰ�����ٶ�С���ҵ��ٶȣ��ڳ�����1Сʱ�������г̾�Ϊ10km���۳�����1.5Сʱ�����г̱��Ҷ�3km���ܼױ����ȵ����յ㣮������ȷ���У�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
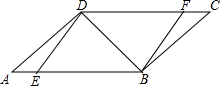 ��ͼ����?ABCD�У���E��F�ֱ���AB��DC�ϣ���ED��DB��FB��BD��
��ͼ����?ABCD�У���E��F�ֱ���AB��DC�ϣ���ED��DB��FB��BD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com