解:(1)(1-

)•

=
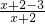
•

=
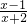
•

=

;
(2)

=

-
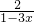
,
变形得:
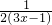
=

+
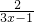
,
方程左右两边同时乘以2(3x-1)得:
1=3x-1+4,
解得:x=-

,
经检验:x=-

是原分式方程的解;
(3)①根据题意列出表格得:
| 1 | 2 | 3 | 4 |
| 1 | (1,1) | (2,1) | (3,1) | (4,1) |
| 2 | (1,2) | (2,2) | (3,2) | (4,2) |
| 3 | (1,3) | (2,3) | (3,3) | (4,3) |
可得出指针所指的两个数字之和所有可能为:2,3,4,5,3,4,5,6,4,5,6,7共12种情况,
其中指针所指的两个数字之和为奇数有6种,
则P
甲获胜=
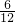
=

;
②公平,理由为:由①得:P
甲获胜=P
乙获胜=

,故游戏公平.
分析:(1)将括号中的两项通分并利用同分母分式的减法法则计算,整理后约分即可得到结果;
(2)将方程左边分式的分母提取2分解因式,右边第二项分母提取-1变形,找出最简公分母为2(3x-1),在方程两边同时乘以2(3x-1)去括号后,转化为整式方程,求出方程的解,经检验即可得到原分式方程的解;
(3)①根据题意列出相应的表格,得到指针所指的两个数字之和所有可能个数,再找出指针所指的两个数字之和为奇数的个数,利用概率公式即可求出甲获胜的概率;
②公平,理由为:根据求出的甲获胜的概率,求出乙获胜的概率,根据两人获胜的概率相等,可得出游戏公平.
点评:此题考查了分式的混合运算,分式方程的解法,以及游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.

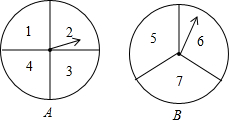 (1)计算
(1)计算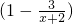 •
•

 )•
)•
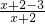 •
•
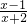 •
•
 ;
; =
= -
-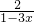 ,
,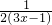 =
= +
+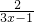 ,
, ,
, 是原分式方程的解;
是原分式方程的解;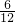 =
= ;
; ,故游戏公平.
,故游戏公平.
