
如图,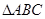 中,
中,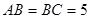 ,
,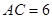 ,过点
,过点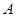 作
作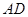 ∥
∥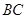 ,点
,点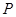 、
、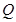 分别是射线
分别是射线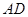 、线段
、线段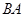 上的动点,且
上的动点,且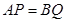 ,过点
,过点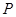 作
作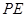 ∥
∥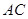 交线段
交线段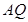 于点
于点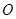 ,联接
,联接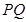 ,设
,设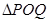 面积为
面积为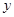 ,
,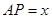 .
.
(1)用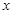 的代数式表示
的代数式表示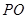 ;
;
(2)求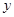 与
与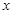 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(3)联接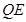 ,若
,若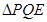 与
与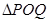 相似,求
相似,求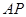 的长.
的长.

(1)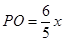 (2)
(2)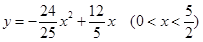 (3)
(3)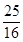
【解析】(1)∵ ∥
∥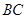 ,
,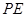 ∥
∥ ,
,
∴四边形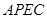 是平行四边形
1分
是平行四边形
1分
∴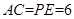 ,
,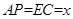 1分
1分
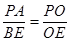 ,
,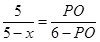 1分
1分
可得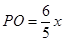 1分
1分
解:(2)∵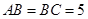 ,
,
∴∠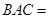 ∠
∠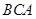
又∠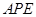 =∠
=∠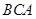 ,∠
,∠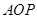 =∠
=∠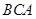 ,
,
∴∠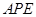 =∠
=∠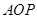 ,
,
∴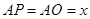 源:学*科*网]
源:学*科*网]
∴当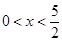 时,
时,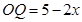 ;
1分
;
1分
作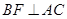 ,
,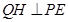 ,垂足分别为点
,垂足分别为点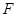 、
、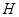 ,
,

则易得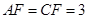 ,
,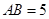 ,
,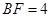 ,
,
由∠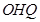 =∠
=∠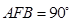 ,∠
,∠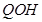 =∠
=∠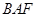
得△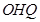 ∽△
∽△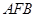
∴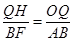 ,
,
∴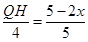 ,
,
∴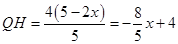 2分
2分
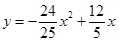 1分
1分
所以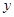 与
与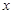 的函数关系式是
的函数关系式是
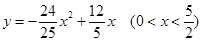 1分
1分
解:(3)【解法一】当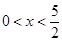 时
时
由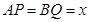 ,
,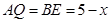 ,∠
,∠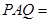 ∠
∠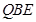
可得△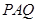 ≌△
≌△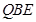 ,于是
,于是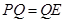 1分
1分
由于∠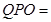 ∠
∠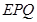 ,
,
所以若△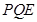 与△
与△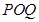 相似,
相似,
只有△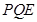 ∽△
∽△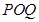
可得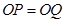 1分
1分
于是得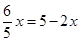 ,解得
,解得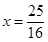 2分
2分
同理当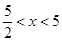 ,可得
,可得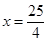 (不合题意,舍去) 1分
(不合题意,舍去) 1分
所以,若△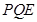 与△POQ相似,AP的长为
与△POQ相似,AP的长为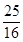 。
。
【解法二】当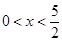 时,可得
时,可得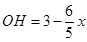 ,
,
于是得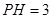 ,
,
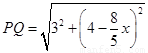 1分
1分
由于∠ =∠
=∠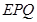 ,
,
所以若△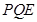 与△
与△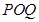 相似,只有△
相似,只有△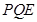 ∽△
∽△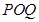
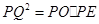 1分
1分
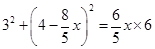
解得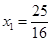 ,
,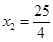 (不合题意,舍去) 2分
(不合题意,舍去) 2分
所以,若△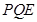 与△
与△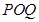 相似,
相似,
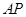 的长为
的长为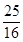 1分
1分
(1)首先根据AD∥BC,PE∥AC,判定四边形APEC是平行四边形,从而得到AC=PE=6,AP=EC=x,然后根据平行线分线段成比例定理列出比例式用含x的代数式表示PO;
(2)根据AB=BC=5,利用等边对等角得到∠BAC=∠BCA,再根据∠APE=∠BCA,∠AOP=∠BCA,得到∠APE=∠AOP,设AP=AO=x,用含x的式子表示OQ=5-2x,利用△OHQ∽△AFB表示出y与x的函数关系式即可;
(3)根据当0<x<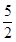 时,由AP=BQ=x,AQ=BE=5-x,∠PAQ=∠QBE可得△PAQ≌△QBE,于是PQ=QE,可得若△PQE与△POQ相似,只有△PQE∽△POQ,于是得
时,由AP=BQ=x,AQ=BE=5-x,∠PAQ=∠QBE可得△PAQ≌△QBE,于是PQ=QE,可得若△PQE与△POQ相似,只有△PQE∽△POQ,于是得 x=5-2x,解得x的值即可.
x=5-2x,解得x的值即可.
|


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2012届上海市金山初三二模数学试卷(带解析) 题型:解答题
如图, 中,
中,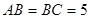 ,
,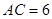 ,过点
,过点 作
作 ∥
∥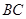 ,点
,点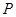 、
、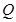 分别是射线
分别是射线 、线段
、线段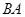 上的动点,且
上的动点,且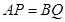 ,过点
,过点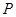 作
作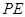 ∥
∥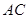 交线段
交线段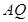 于点
于点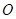 ,联接
,联接 ,设
,设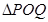 面积为
面积为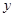 ,
, .
.
(1)用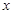 的代数式表示
的代数式表示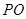 ;
;
(2)求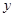 与
与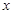 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(3)联接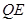 ,若
,若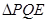 与
与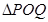 相似,求
相似,求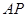 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江省八里店一中九年级第二学期期中考试数学试卷(带解析) 题型:解答题
如图,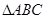 中,
中, ,
,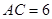 ,过点
,过点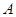 作
作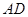 ∥
∥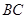 ,点
,点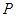 、
、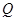 分别是射线
分别是射线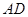 、线段
、线段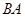 上的动点,且
上的动点,且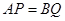 ,过点
,过点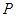 作
作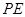 ∥
∥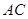 交线段
交线段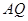 于点
于点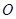 ,联接
,联接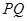 ,设
,设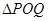 面积为
面积为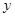 ,
,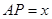 .
.
(1)用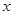 的代数式表示
的代数式表示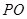 ;
;
(2)求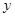 与
与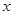 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(3)联接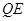 ,若
,若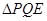 与
与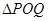 相似,求
相似,求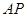 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:2013届浙江省九年级第二学期期中考试数学试卷(解析版) 题型:解答题
如图,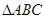 中,
中,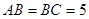 ,
,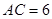 ,过点
,过点 作
作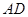 ∥
∥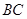 ,点
,点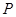 、
、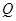 分别是射线
分别是射线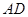 、线段
、线段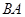 上的动点,且
上的动点,且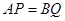 ,过点
,过点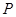 作
作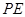 ∥
∥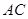 交线段
交线段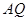 于点
于点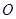 ,联接
,联接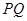 ,设
,设 面积为
面积为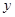 ,
,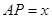 .
.

(1)用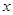 的代数式表示
的代数式表示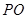 ;
;
(2)求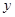 与
与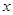 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(3)联接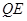 ,若
,若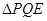 与
与 相似,求
相似,求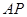 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:2010-2011学年南京市考数学一模试卷 题型:解答题
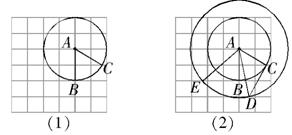
(本题12分) 在正方形网格中以点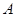 为圆心,
为圆心,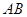 为半径作圆
为半径作圆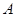 交网格于点
交网格于点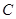 (如图(1)),过点
(如图(1)),过点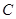 作圆的切线交网格于点
作圆的切线交网格于点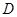 ,以点
,以点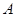 为圆心,
为圆心,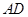 为半径作圆交网格于点
为半径作圆交网格于点
(如图(2)).
 问题:
问题:
(1)求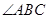 的度数;
的度数;
(2)求证: 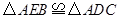 ;
;
(3)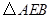 可以看作是由
可以看作是由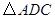 经过怎样的变换得到的?并判断
经过怎样的变换得到的?并判断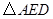 的形状(不用说明理由).
的形状(不用说明理由).
(4)如图(3),已知直线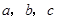 ,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形
,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形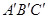 ,使三个顶点
,使三个顶点 ,分别在直线
,分别在直线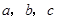 上.要求写出简要的画图过程,不需要说明理由.
上.要求写出简要的画图过程,不需要说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com