
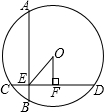
 如图,⊙O的弦AB⊥CD于E,OF⊥CD于F,且OF=2,OE=4,OA=
如图,⊙O的弦AB⊥CD于E,OF⊥CD于F,且OF=2,OE=4,OA=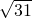 .
.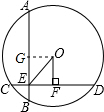 解:(1)过点O作OG⊥AB于G,连接OA,则AG=BG=
解:(1)过点O作OG⊥AB于G,连接OA,则AG=BG= AB,
AB,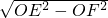 =
= =2
=2
 ,
,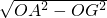 =
= =
= ,
, .
. AB=
AB= ×2
×2 =
= ,
, -2.
-2. AB,再根据OF⊥CD,AB⊥CD可知四边形OFEG是矩形,再在Rt△OEF、Rt△OAG中利用勾股定理可求出EF及AG的长,故可得出AB的长;
AB,再根据OF⊥CD,AB⊥CD可知四边形OFEG是矩形,再在Rt△OEF、Rt△OAG中利用勾股定理可求出EF及AG的长,故可得出AB的长; AB可得出BG的长,再根据BE=BG-EG即可得出结论.
AB可得出BG的长,再根据BE=BG-EG即可得出结论.

 优等生题库系列答案
优等生题库系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com