
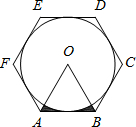
 (2012•咸宁)如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为( )
(2012•咸宁)如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为( ) 解:∵六边形ABCDEF是正六边形,
解:∵六边形ABCDEF是正六边形,
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
60×π×(
| ||
| 360 |
| 3 |
| π |
| 2 |


科目:初中数学 来源: 题型:
 (2012•咸宁)如图,在梯形ABCD中,AD∥BC,∠C=90°,BE平分∠ABC且交CD于E,E为CD的中点,EF∥BC交AB于F,EG∥AB交BC于G,当AD=2,BC=12时,四边形BGEF的周长为
(2012•咸宁)如图,在梯形ABCD中,AD∥BC,∠C=90°,BE平分∠ABC且交CD于E,E为CD的中点,EF∥BC交AB于F,EG∥AB交BC于G,当AD=2,BC=12时,四边形BGEF的周长为查看答案和解析>>
科目:初中数学 来源: 题型:
 转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D.运动时间为t秒.
转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D.运动时间为t秒.| 25 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•咸宁)如图,某公园入口处原有三级台阶,每级台阶高为18cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是
(2012•咸宁)如图,某公园入口处原有三级台阶,每级台阶高为18cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•咸宁)如图,一次函数y1=kx+b的图象与反比例函数y2=
(2012•咸宁)如图,一次函数y1=kx+b的图象与反比例函数y2=| m | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•咸宁)如图,AB是⊙O的直径,点E是AB上的一点,CD是过E点的弦,过点B的切线交AC的延长线于点F,BF∥CD,连接BC.
(2012•咸宁)如图,AB是⊙O的直径,点E是AB上的一点,CD是过E点的弦,过点B的切线交AC的延长线于点F,BF∥CD,连接BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com