练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知y+3与x+2成正比例，且当x＝3时，y＝7．
    (1)写出y与x之间的函数关系式；
    (2)当x＝－1时，求y的值；
    (3)当y＝0时，求x的值．

    (1)y=2x+1；(2)-1；(3).

    解析试题分析：(1)已知y+3与x+2成正比例，所以，设y+3="k(" x+2),把x＝3，y＝7代入求出k的值，即可写出y与x之间的函数关系式，
    (2)把x＝－1代入y与x之间的函数关系式，求出y的值.
    (3)把y＝0代入y与x之间的函数关系式，求出x的值．
    试题解析:(1)y=2x+1
    (2)x=-1时y= -1
    (3)y=0时x=
    考点：1.正比例函数关系式.2.函数值和自变量值.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    如图：一次函数的图象与反比例函数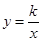的图象交于A（－2,6）和点B（4,n）

    （1）求反比例函数的解析式和B点坐标
    （2）根据图象回答,在什么范围时,一次函数的值大于反比例函数的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，一次函数与反比例函数的图象交于A（2，1），B（-1，）两点．

    （1）求m、k、b的值；
    （2）连接OA、OB，计算三角形OAB的面积；
    （3）结合图象直接写出不等式的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，直线y＝kx－2与x轴、y轴分别交于B、C两点，OB：OC＝．
     
    (1)求B点的坐标和k的值．
    (2)若点A(x，y)是第一象限内的直线y＝kx－2上的一个动点，当点A运动过程中，①试写出△AOB的面积S与x的函数关系式；②探索：当点A运动到什么位置时，△AOB的面积是1.③在②成立的情况下，x轴上是否存在一点P，使△POA是等腰三角形．若存在，请写出满足条件的所有P点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，已知直线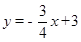与x轴、y轴分别交于点A、B，线段AB为直角边在第一象限内作等腰Rt△ABC，∠BAC=90°.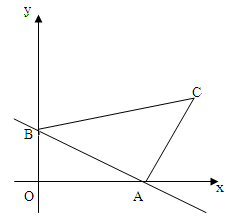

    （1）求△AOB的面积；
    （2）求点C坐标；
    （3）点P是x轴上的一个动点，设P（x,0）
    ①请用x的代数式表示PB2、PC2；
    ②是否存在这样的点P，使得|PC-PB|的值最大？如果不存在，请说明理由；
    如果存在，请求出点P的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，两摞相同规格的饭碗整齐地叠放在桌面上，请根据图中给的数据信息，解答下列问题：

    （1）求整齐摆放在桌面上饭碗的高度y（cm）与饭碗数x（个）之间的一次函数解析式；
    （2）把这两摞饭碗整齐地摆成一摞时，这摞饭碗的高度是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    国家推行“节能减排，低碳经济”的政策后，某企业推出一种叫“CNG”的改烧汽油为天然气的装置，每辆车改装费为b元.据市场调查知：每辆车改装前、后的燃料费（含改装费）、（单位：元）与正常运营时间（单位：天）之间分别满足关系式：、，如图所示.

    试根据图像解决下列问题：
    （1）每辆车改装前每天的燃料费=     元,每辆车的改装费b=    元.正常运营    天后，就可以从节省燃料费中收回改装成本.
    （2）某出租汽车公司一次性改装了100辆车，因而，正常运营多少天后共节省燃料费40万元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，一次函数y=kx+1（k≠0）与反比例函数（m≠0）的图象有公共点A（1，2）．直线l⊥x轴于点N（3，0），与一次函数和反比例函数的图象分别交于点B，C．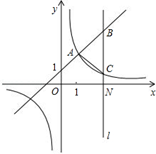

    （1）求一次函数与反比例函数的解析式；
    （2）求△ABC的面积？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，直线MN与x轴，y轴分别相交于A，C两点，分别过A，C两点作x轴，y轴的垂线相交于B点，且OA，OC（OA＞OC）的长分别是一元二次方程x2﹣14x+48=0的两个实数根．

    （1）求C点坐标；
    （2）求直线MN的解析式；
    （3）在直线MN上存在点P，使以点P，B，C三点为顶点的三角形是等腰三角形，请直接写出P点的坐标．

    查看答案和解析>>

    同步练习册答案