练习册

  • 练习册
  • 试题
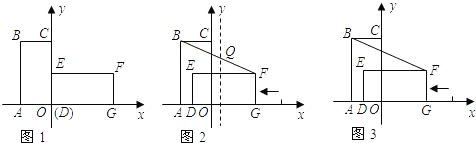
    精英家教网 > 初中数学 > 题目详情
    如图所示，请你探索正方形的个数与等腰三角形的个数之间的关系．

    （1）照这样的画法，如果画15个正方形，可以得
    56
    56
    个等腰三角形；
    （2）若要得到152个等腰三角形，应画
    39
    39
    个正方形；
    分析：从图中所给出的四个例子可知，当正方形个数为1时，等腰三角形的个数为0，当正方形的个数为2时，等腰三角形的个数为4，当正方形个数为3时，等腰三角形的个数为8，当正方形的个数为4时，等腰三角形的个数为12，从而可以得出规律当正方形的个数为n时，等腰三角形的个数为4（n-1）．
    解答：解：从图中可以得出如下规律：当正方形的个数为n时，等腰三角形的个数为4（n-1）．
    （1）当正方形的个数为15时，等腰三角形的个数为4（15-1）=56；
    （2）由题意可知当正方形的个数为n时，等腰三角形的个数为4（n-1）．
    ∴4（n-1）=152，可得n=39．
    点评：本题考查同学们看图的能力，解题的关键是找出其中的规律．了解等腰三角形的性质．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    在平面直角坐标系中，矩形OABC的边OA在x轴的负半轴上，边OC在y轴的正半轴上，且OA=1，OC=2．将矩形OABC绕点O顺时针旋转90°，得到矩形DEFG（如图1）．
    （1）若抛物线y=-x2+bx+c经过点B和F，求此抛物线的解析式；
    （2）将矩形DEFG以每秒1个单位长度的速度沿x轴负方向平移，平移t秒时，所成图形如图2所示．
    ①图2中，在0＜t＜1的条件下，连接BF，BF与（1）中所求抛物线的对称轴交于点Q，设矩形DEFG与矩形OABC重合部分的面积为S1，△AQF的面积为S2，试判断S1+S2的值是否发生变化？如果不变，求出其值；
    ②在0＜t＜3的条件下，P是x轴上一点，请你探究：是否存在t值，使以PB为斜边的Rt△PFB与Rt△AOC相似？若存在，直接写出满足条件t的值及点P的坐标；若不存在，请说明理由（利用图3分析探索）．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1）如图1，是某市公园周围街巷的示意图，A点表示1街与2巷的十字路口，B点表示3街与5巷的十字路口，如果用（1，2）→（2，2）→（3，2）→（3，3）→（3，4）→（3，5）表示由A点到B点的一条路径，那么，你能同样的方法写出由A点到B点尽可能近的其他两条路径吗？

    （2）从正三角形、正四边形、正五边形、正六边形、正八边形、正十边形、正十二边形中任选两种正多边形镶嵌，请全部写出这两种正多边形．并从其中任选一种探索这两种正多边形共能镶嵌成几种不同的平面图形？说明你的理由．
    （3）如图2所示，已知AB∥CD，分别探索下列四个图形中∠P（均为小于平角的角）与∠A，∠C的关系，请你从所得的四个关系中任选一个加以说明．
    （4）阅读材料：多边形上或内部的一点与多边形各顶点的连线，将多边形分割成若干个小三角形．如图3给出了四边形的具体分割方法，分别将四边形分割成了2个、3个、4个小三角形．
    请你按照上述方法将图4中的六边形进行分割，并写出得到的小三角形的个数以及求出每个图形中的六边形的内角和．试把这一结论推广至n边形，并推导出n边形内角和的计算公式．

    查看答案和解析>>

    科目：初中数学 来源：新教材新学案数学九年级上册 题型：059

    已知正方形ABCD的边长AB＝k(k是正整数)，正△PAE的顶点P在正方形内，顶点E在边AB上，且AE＝1．将△PAE在正方形内按图中所示的方式，沿着正方形的边AB，BC，CD，DA，AB…连续地翻转n次，使顶点P第一次回到原来的起始位置．

    (1)

    如果我们把正方形ABCD的边展开在一直线上，那么这一翻转过程可以看作是△PAE在直线上作连续的翻转运动．如图是k＝1时，△PAE沿正方形的边连续翻转过程的展开示意图．请你探索：若k＝1，则△PAE沿正方形的边连续翻转的次数n＝________时，顶点P第一次回到原来的起始位置．

    (2)

    若k＝2，则n＝________时，顶点P第一次回到原来的起始位置；若k＝3，则n＝________时，顶点P第一次回到原来的起始位置．

    (3)

    请你猜测：使顶点P第一次回到原来的起始位置的n值与k之间的关系(请用含k的代数式表示n)．

    查看答案和解析>>

    科目：初中数学 来源：第2章《二次函数》中考题集（35）：2.4 二次函数的应用（解析版） 题型：解答题

    在平面直角坐标系中，矩形OABC的边OA在x轴的负半轴上，边OC在y轴的正半轴上，且OA=1，OC=2．将矩形OABC绕点O顺时针旋转90°，得到矩形DEFG（如图1）．
    （1）若抛物线y=-x2+bx+c经过点B和F，求此抛物线的解析式；
    （2）将矩形DEFG以每秒1个单位长度的速度沿x轴负方向平移，平移t秒时，所成图形如图2所示．
    ①图2中，在0＜t＜1的条件下，连接BF，BF与（1）中所求抛物线的对称轴交于点Q，设矩形DEFG与矩形OABC重合部分的面积为S1，△AQF的面积为S2，试判断S1+S2的值是否发生变化？如果不变，求出其值；
    ②在0＜t＜3的条件下，P是x轴上一点，请你探究：是否存在t值，使以PB为斜边的Rt△PFB与Rt△AOC相似？若存在，直接写出满足条件t的值及点P的坐标；若不存在，请说明理由（利用图3分析探索）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

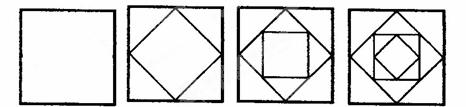
    （1）如图所示，请你探索正方形与等腰三角形的个数之间的关系后填下表。

    正   正方形个数

    11   1

    22   2  

    33   3

    44   4

    ··     ···

    等  等腰三角形个数

    0

    ·      ···

    （2）若正方形的个数为n时，等腰三角形有___________ 个。

    （3）若要得到152个等腰三角形，应画_____________个正方形；

    查看答案和解析>>

    同步练习册答案