
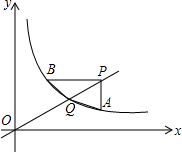
 如图,直线y=mx与反比例函数y=$\frac{k}{x}$(x>0)的图象交于Q点,点A,点B都在反比例函数y=$\frac{k}{x}$的图象上,点P在OQ延长线上,且PA∥y轴,PB∥x轴,且连结AQ,BQ,已知B(3,4).
如图,直线y=mx与反比例函数y=$\frac{k}{x}$(x>0)的图象交于Q点,点A,点B都在反比例函数y=$\frac{k}{x}$的图象上,点P在OQ延长线上,且PA∥y轴,PB∥x轴,且连结AQ,BQ,已知B(3,4).分析 (1)由点B可得反比例函数解析式,继而可得点A的坐标,根据PA∥y轴,PB∥x轴知点P坐标,即可求直线OP解析式;
(2)由O、B、P三点坐标求得OB、OP、BP的长,根据S△BOP=$\frac{1}{2}$BP•yP=$\frac{1}{2}$OB•OP•sin∠BOP可求得sin∠BOP的值;
(3)已知B(3,4),设P($\frac{4}{m}$,4),A($\frac{4}{m}$,3m),联立方程组求得点Q坐标,表示出$\frac{{S}_{△APQ}}{{S}_{△BPQ}}$整理化简即可知.
解答 解:(1)∵B(3,4)在y=$\frac{k}{x}$的图象上,
∴4=$\frac{k}{3}$,
∴k=12,
∴y=$\frac{12}{x}$,
当y=$\frac{9}{4}$时,x=$\frac{16}{3}$,
∴A($\frac{16}{3}$,$\frac{9}{4}$).
∵PA∥y轴,PB∥x轴,
∴P($\frac{16}{3}$,4).
代入y=mx,得$\frac{16}{3}$m=4,
∴m=$\frac{3}{4}$,
∴y=$\frac{3}{4}$x;
(2)∵B(3,4),P($\frac{16}{3}$,4),
∴OB=$\sqrt{{3}^{2}+{4}^{2}}$,OP=$\sqrt{(\frac{16}{3})^{2}+{4}^{2}}$=$\frac{20}{3}$,BP=$\frac{16}{3}$-3=$\frac{7}{3}$.
∵S△BOP=$\frac{1}{2}$BP•yP=$\frac{1}{2}$OB•OP•sin∠BOP,
∴sin∠BOP=$\frac{BP•{y}_{P}}{OB•OP}$=$\frac{7}{25}$;
(3)由题意,得B(3,4),P($\frac{4}{m}$,4),A($\frac{4}{m}$,3m).
解$\left\{\begin{array}{l}{y=\frac{12}{m}}\\{y=mx}\end{array}\right.$得Q($\frac{2\sqrt{3}}{\sqrt{m}}$,2$\sqrt{3m}$)
∴$\frac{{S}_{△APQ}}{{S}_{△BPQ}}$=$\frac{\frac{1}{2}(4-3m)(\frac{4}{m}-\frac{2\sqrt{3}}{\sqrt{m}})}{\frac{1}{2}(\frac{4}{m}-3)(4-2\sqrt{3m})}$=$\frac{\frac{1}{m}(4-3m)(4-2\sqrt{m})}{\frac{1}{m}(4-3m)(4-2\sqrt{m})}$=1,
∴$\frac{{S}_{△APQ}}{{S}_{△BPQ}}$的值不变,为1.
点评 本题主要考查反比例函数与一次函数交点问题,根据已知条件表示出或设出相关点的坐标是根本,掌握交点坐标的求法及三角形面积的不同求法是解题关键.


科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y3<y2<y1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
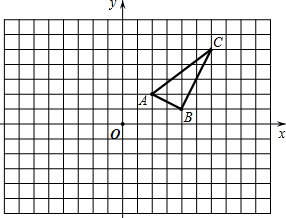
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com