
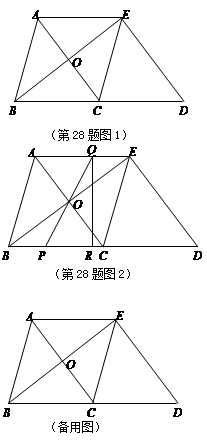
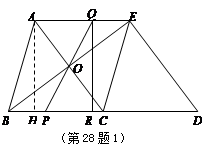 =×BE×ED=×8×6=24. ---------------6分
=×BE×ED=×8×6=24. ---------------6分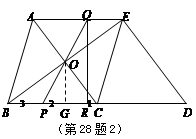 |


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源:不详 题型:解答题
 ,
, .
.
 垂直于线段
垂直于线段 .设图(1)、图(2)和图(3)中的四边形
.设图(1)、图(2)和图(3)中的四边形 的
的 ,
, 和
和 ,则
,则 = ,
= , = ,
= , = ;
= ; 与线段
与线段 垂直相交(垂足
垂直相交(垂足 不与点
不与点 ,
, ,
, ,
, 重合)的任意情形,请你就四边形
重合)的任意情形,请你就四边形 面积的大小提出猜想,并证明你的猜想.
面积的大小提出猜想,并证明你的猜想.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
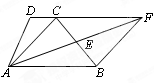
 ,PA:PB=1:3,则PQ=__________;
,PA:PB=1:3,则PQ=__________; =__________。
=__________。查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 如图1,在△ABC中,AB=BC=5,AC="6." △ECD是△ABC沿BC方向平移得到的,连接AE. AC和BE相交于点O.
如图1,在△ABC中,AB=BC=5,AC="6." △ECD是△ABC沿BC方向平移得到的,连接AE. AC和BE相交于点O.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com