
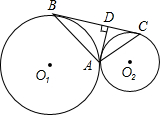
 如图,⊙O1(R)与⊙O2(r)外切于点A,BC是外公切线.求证:
如图,⊙O1(R)与⊙O2(r)外切于点A,BC是外公切线.求证:分析 (1)如图1,作O1E⊥AB于E,O2F⊥AC于F,连接BO1,CO2,由垂径定理得到BE=$\frac{1}{2}$AB,CF=$\frac{1}{2}$AC,∠O1BA=∠DAB,根据相似三角形的性质得到AB2=2AD•R,同理可得,AC2=2AD•r,于是得到结论;
(2)如图2,作两圆的内公切线交BC于D,连接BO1,CO2,过O2作O2E⊥BO1于E,则BC=O2E,根据勾股定理得到BC=O2E=$\sqrt{(r+R)^{2}+(R-r)^{2}}$=2$\sqrt{Rr}$,根据切线的性质得到AD=BD=CD,推出△ABC是直角三角形,由勾股定理得到BC2=AC2+AB2,于是得到结论.
解答 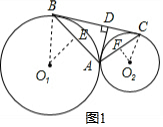 解:(1)如图1,作O1E⊥AB于E,O2F⊥AC于F,连接BO1,CO2,
解:(1)如图1,作O1E⊥AB于E,O2F⊥AC于F,连接BO1,CO2,
∴BE=$\frac{1}{2}$AB,CF=$\frac{1}{2}$AC,∠O1BA=∠DAB,
∴△BDA∽△O1EB,
∴BA:O1B=DA:EB,即BA:R=DA:$\frac{1}{2}$AB,
∴AB2=2AD•R,
同理可得,AC2=2AD•r,
∴$\frac{A{B}^{2}}{A{C}^{2}}$=$\frac{R}{r}$;
(2)如图2,作两圆的内公切线交BC于D,连接BO1,CO2,过O2作O2E⊥BO1于E,
则BC=O2E,
∴BC=O2E=$\sqrt{(r+R)^{2}+(R-r)^{2}}$=2$\sqrt{Rr}$,
∵⊙O1(R)与⊙O2(r)外切于点A,BC是外公切线,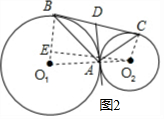
∴AD=BD=CD,
∴△ABC是直角三角形,
∴BC2=AC2+AB2,
∵$\frac{A{B}^{2}}{A{C}^{2}}$=$\frac{R}{r}$,
∴AC2=$\frac{A{B}^{2}•r}{R}$,
∴$\frac{A{B}^{2}•r}{R}$+AB2=4Rr,
∴AB=2R$\sqrt{\frac{r}{R+r}}$.
点评 本题考查了圆与圆的位置关系,切线的性质,勾股定理,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
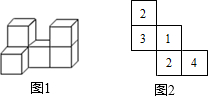 (1)用6个小正方体搭成的立体图形如图1所示,请你画出从它的正面、左面和上面看到的形状图.
(1)用6个小正方体搭成的立体图形如图1所示,请你画出从它的正面、左面和上面看到的形状图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 用水量 | 单价(元/吨) |
| 不超过40吨的部分 | 1.8 |
| 超过40吨的部分 | 2.2 |
| 另:每吨用水加收0.2元的城市污水处理费 | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某印刷厂的厂门上方是一段抛物线,抛物线的顶点离地面的高度是3.8m.一辆装满货物的卡车宽为1.6m,高为2.6m.已知卡车的上端与门的距离不得小于0.2m,这辆卡车能否通过厂门?
如图,某印刷厂的厂门上方是一段抛物线,抛物线的顶点离地面的高度是3.8m.一辆装满货物的卡车宽为1.6m,高为2.6m.已知卡车的上端与门的距离不得小于0.2m,这辆卡车能否通过厂门?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com