
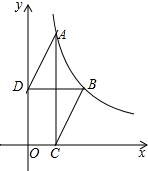
 如图,函数y=$\frac{k}{x}(x>0)$的图象经过点A,B,点B的坐标为(1,1),过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,连接AD,BC.若AD∥BC,则线段BC的长度为$\frac{\sqrt{5}}{2}$.
如图,函数y=$\frac{k}{x}(x>0)$的图象经过点A,B,点B的坐标为(1,1),过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,连接AD,BC.若AD∥BC,则线段BC的长度为$\frac{\sqrt{5}}{2}$. 分析 由点B(1,1)求得y=$\frac{1}{x}$,设A点的坐标为:(m,$\frac{1}{m}$),则C点的坐标为:(m,0),tan∠ADF=$\frac{AF}{DF}$=$\frac{\frac{1}{m}-1}{m}$,tan∠AEC=$\frac{AC}{EC}$=$\frac{\frac{1}{m}}{1}$=$\frac{1}{m}$,进而求出m的值,即可得出答案.
解答 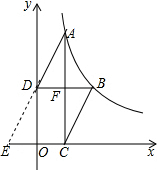 解:延长AD交x轴于E,设AC,BD交于F,
解:延长AD交x轴于E,设AC,BD交于F,
∵点B(1,1)在函数y=$\frac{k}{x}$(x>0)的图象上,
∴k=1,则y=$\frac{1}{x}$,
设A点的坐标为:(m,$\frac{1}{m}$),则C点的坐标为:(m,0),
∵BD∥CE,且BC∥DE,
∴四边形BCED为平行四边形,
∴CE=BD=1,
∵BD∥CE,
∴∠ADF=∠AEC,
∴在Rt△AFD中,tan∠ADF=$\frac{AF}{DF}$=$\frac{\frac{1}{m}-1}{m}$,
在Rt△ACE中,tan∠AEC=$\frac{AC}{EC}$=$\frac{\frac{1}{m}}{1}$=$\frac{1}{m}$,
∴$\frac{\frac{1}{m}-1}{m}=\frac{1}{m}$,
解得:m=$\frac{1}{2}$,
∴C点的坐标为:($\frac{1}{2}$,0),
则BC=$\frac{\sqrt{5}}{2}$,
故答案为:$\frac{\sqrt{5}}{2}$.
点评 此题主要考查了反比例函数与一次函数的交点以及锐角三角函数关系等知识,得出A,D点坐标是解题关键.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:选择题
| A. | 抛掷1个均匀的骰子,出现4点向上 | |
| B. | 任意数的绝对值都是正数 | |
| C. | 两直线被第三条直线所截,内错角相等 | |
| D. | 13人中至少有2人的生日在同一个月 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16 | B. | 17 | C. | 18 | D. | 19 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
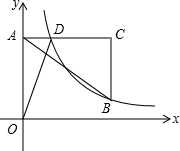 如图,在平面直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B、C的横坐标都是3,且BC=2,点D在AC上,若反比例函数$y=\frac{k}{x}(x>0)$的图象经过点B、D,且$\frac{AO}{BC}=\frac{3}{2}$.
如图,在平面直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B、C的横坐标都是3,且BC=2,点D在AC上,若反比例函数$y=\frac{k}{x}(x>0)$的图象经过点B、D,且$\frac{AO}{BC}=\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
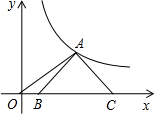 如图,等腰Rt△ABC的斜边BC在x轴上,顶点A在反比例函数$y=\frac{3}{x}(x>0)$的图象上,连接OA,若OB=2,则点A的坐标为(3,1).
如图,等腰Rt△ABC的斜边BC在x轴上,顶点A在反比例函数$y=\frac{3}{x}(x>0)$的图象上,连接OA,若OB=2,则点A的坐标为(3,1).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
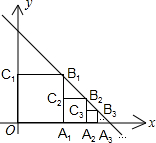 正方形OA1B1C1、A1A2B2C2、A2A3B3C3┅按如图放置,其中点A1、A2、A3┅在x轴的正半轴上,点B1、B2、B3┅在直线y=-x+2上,则点A3的坐标为($\frac{7}{4}$,0),则点An的坐标为($\frac{{2}^{n}-1}{{2}^{n-1}}$,0).
正方形OA1B1C1、A1A2B2C2、A2A3B3C3┅按如图放置,其中点A1、A2、A3┅在x轴的正半轴上,点B1、B2、B3┅在直线y=-x+2上,则点A3的坐标为($\frac{7}{4}$,0),则点An的坐标为($\frac{{2}^{n}-1}{{2}^{n-1}}$,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com