
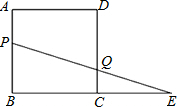
 线上,CE=BC,连接PE交CD于点Q.
线上,CE=BC,连接PE交CD于点Q.| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 360 |
| n |
| 360 |
| n |
| s |
| n |
| KM |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
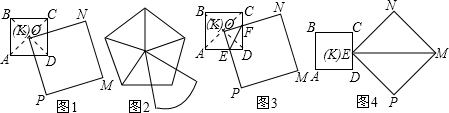
 已知,如图,正方形ABCD中,点E、F分别在边BC、CD上,且∠EAF=45°,AG⊥EF于G,EG=2,FG=3,求AG的边长.小萍同学灵活运用旋转的知识,将图形进行旋转变换,巧妙地解答了此题.请按照小萍的思路,探究并解答下列问题:
已知,如图,正方形ABCD中,点E、F分别在边BC、CD上,且∠EAF=45°,AG⊥EF于G,EG=2,FG=3,求AG的边长.小萍同学灵活运用旋转的知识,将图形进行旋转变换,巧妙地解答了此题.请按照小萍的思路,探究并解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 附加题:(成绩只作参考,不计入总分)
附加题:(成绩只作参考,不计入总分)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
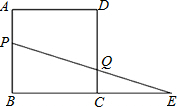 线上,CE=BC,连接PE交CD于点Q.
线上,CE=BC,连接PE交CD于点Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com