
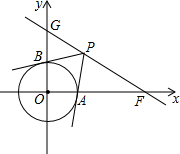
 如图,在平面直角坐标系中,O为坐标原点,已知点F(2$\sqrt{3}$,0),直角GF交y轴正半轴于点G,且∠GFO=30°.
如图,在平面直角坐标系中,O为坐标原点,已知点F(2$\sqrt{3}$,0),直角GF交y轴正半轴于点G,且∠GFO=30°.分析 (1)由已知条件得到OF=2$\sqrt{3}$,解直角三角形即可得到结论;
(2)①连接OPOP,根据切线的性质得到OB⊥PB,当OP⊥GF时,线段PO最短,解直角三角形得到OP=$\sqrt{3}$,PB=$\sqrt{O{P}^{2}-O{B}^{2}}$=$\sqrt{(\sqrt{3})^{2}-{1}^{2}}$=2;
②根据切线的性质和角平分线的定义得到∠OPB=30°,求得OP=2,点P是以点O为圆心,2为半径的圆与直线GF的交点,由于点P1与点G(0,2)重合,即P1(0,2),推出△GOP2是等边三角形求得FP2=2,即可得到结论.
解答 解:(1)∵F(2$\sqrt{3}$,0),
∴OF=2$\sqrt{3}$,
∵∠GFO=30°,
∴OG=2,
∴点G的坐标是(0,2);
(2)①连接OPOP,如图,
∵PB切⊙OO于点BB,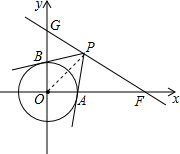
∴OB⊥PB,
根据勾股定理得PB2=OP2-OB2,
∵OB=1,
∴要使BP的值最小,则需OP的值最小,当OP⊥GF时,线段PO最短,
在Rt△PFO,OF=2$\sqrt{3}$,∠GFO=30°,
∴OP=$\sqrt{3}$,
∴PB=$\sqrt{O{P}^{2}-O{B}^{2}}$=$\sqrt{(\sqrt{3})^{2}-{1}^{2}}$=$\sqrt{2}$;
②存在,
∵PA、PB均与⊙O相切,
∴OP平分∠APB,
∵∠APB=60°,
∴∠OPB=30°,
∵OB=1,∴OP=2,
∴点P是以点O为圆心,2为半径的圆与直线GF的交点,
即图中的P1、P2两点,连接OP2,
∵OG=2,
∴点P1与点G(0,2)重合,即P1(0,2),
在Rt△GOF中,∠GFO=30°,
∴∠OGF=60°,
∵OG=OP2,
∴△GOP2是等边三角形,
∴GP2=OG=2,已知GF=4,
∴FP2=2,
∴P2为GF的中点,
∴P2($\sqrt{3}$,1),
综上所述,满足条件的点P的坐标为(0,2)或($\sqrt{3}$,1).
点评 本题考查了切线的性质,勾股定理角平分线的性质,等边三角形的判定和性质,熟练掌握切线的性质是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 52和54 | B. | 52 | C. | 53 | D. | 54 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB是⊙O的直径,弦CD⊥AB于点C,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2.AF=3.给出下列结论:
如图,AB是⊙O的直径,弦CD⊥AB于点C,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2.AF=3.给出下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
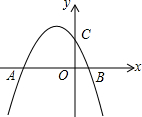 已知抛物线y=-$\frac{1}{2}{x^2}$+bx+c与y轴交于点C,与x轴的两个交点分别为A(-4,0),B(1,0).
已知抛物线y=-$\frac{1}{2}{x^2}$+bx+c与y轴交于点C,与x轴的两个交点分别为A(-4,0),B(1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
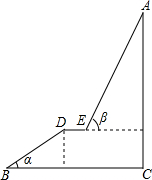 如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,AC=200.4米,BD=100米,∠α=30°,∠β=70°,则AE的长度约为160米.(参考数据:sin70≈0.94,cos70°≈0.34,tan70°≈2.25).
如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,AC=200.4米,BD=100米,∠α=30°,∠β=70°,则AE的长度约为160米.(参考数据:sin70≈0.94,cos70°≈0.34,tan70°≈2.25).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com