
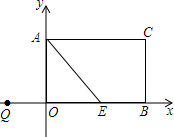
 如图,矩形AOBC,A(0,3)、B(5,0),点E在OB上,∠AEO=45°,点P从点Q(-3,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t (t≥0)秒.
如图,矩形AOBC,A(0,3)、B(5,0),点E在OB上,∠AEO=45°,点P从点Q(-3,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t (t≥0)秒.分析 (1)在Rt△AOE中求出OE,即可得出点E的坐标;
(2)如图1所示,当∠PAE=15°时,可得∠APO=60°,从而可求出PO=$\sqrt{3}$,求出QP,即可得出t的值;
(3)以点P为圆心,PA为半径的⊙P与四边形AEBC的边(或边所在的直线)相切时,只有一种情况,也就是⊙P与AE边相切,且切点为点A,如图2所示,求出PE,得出QP,继而可得t的值.
解答 解:(1)在Rt△AOE中,OA=3,∠AEO=45°,
∴OE=AO=3,
∴点E的坐标为(3,0);
(2)如图1所示: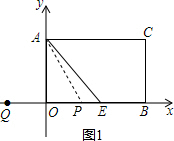
∵∠PAE=15°,∠AEO=45°,
∴∠APO=∠PAE+∠AEO=60°,
∴OP=AOtan30°=$\sqrt{3}$,
∴QP=3+$\sqrt{3}$,
∴t=3+$\sqrt{3}$(秒);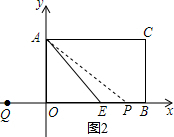
如图2,∵∠AEO=45°,∠PAE=15°,
∴∠APE=30°,
∵AO=3,
∴OP=3÷$\frac{\sqrt{3}}{3}$=3$\sqrt{3}$,
∴t=QP=OQ+OP=(3$\sqrt{3}$+3)s;
∴t=(3+$\sqrt{3}$)s或(3+3$\sqrt{3}$)s.
(3)∵PA是⊙P的半径,且⊙P与AE相切,
∴点A为切点,如图3所示: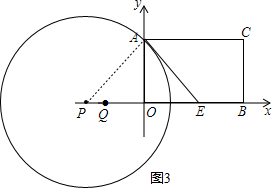
∵AO=3,∠AEO=45°,
∴AE=3$\sqrt{2}$
∴PE=$\frac{AE}{cos45°}$=$\frac{3\sqrt{2}}{\frac{\sqrt{2}}{2}}$=6,
∴QP=QE-PE=6-6=0,
∴当⊙P与四边形AEBC的边AE相切时,Q,P重合,t的值为0.
∵PA是⊙P的半径,且⊙P与AE相切,
∴点A为切点,如图4所示: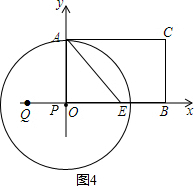
当点P与O重合时,⊙P与AC相切,
∴t=3秒;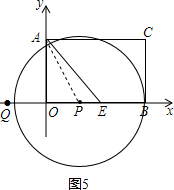
当PA=PB时,⊙P与BC相切,
设OP=x,则PB=PA=5-x,
在Rt△OAP中,x2+32=(5-x)2,
解得:x=1.6,
∴t=3+1.6=4.6(秒);
∴t=0或3或4.6秒时,⊙P与四边形AEBC的边(或边所在的直线)相切.
点评 本题考查了圆的综合,涉及了圆与直线的位置关系、锐角三角函数的定义及外角的性质,难点在第三问,关键是判断出符合题意的情况,然后画出图形,难度较大.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 抛掷总次数 | 100 | 150 | 200 | 300 |
| 杯口朝上的频数 | 21 | 32 | 44 | 66 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
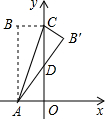 如图,矩形ABCO中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB′C,AB′交y轴于D点,则B′点的坐标为($\frac{42}{29}$,$\frac{105}{29}$).
如图,矩形ABCO中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB′C,AB′交y轴于D点,则B′点的坐标为($\frac{42}{29}$,$\frac{105}{29}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com