
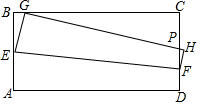
 在矩形纸片ABCD中,AB=2,BC=4,E为AB上一点,F为CD上一点.将矩形纸片沿EF折叠,使得点A恰落在线段BC上,标为点G.
在矩形纸片ABCD中,AB=2,BC=4,E为AB上一点,F为CD上一点.将矩形纸片沿EF折叠,使得点A恰落在线段BC上,标为点G.分析 (1)如图1,利用勾股定理在Rt△BEG中列式可求得y关于x的关系式;如图2时,当F与D重合时,BG的值最大,
求出此时的最大值为:x=AE=4-2$\sqrt{3}$,写出结论;
(2)证明△BEG∽△CGP和△BEG∽△HFP,列比例式,再把y=$\frac{1}{4}{x}^{2}$+1代入即可得出z关于x的关系式;
(3)由∠PMD=30°,可依次推得:∠BEG=30°,则EG=2BG,即y=2x,得方程为:$\frac{1}{4}{x}^{2}$+1=2x,解出即可.
解答 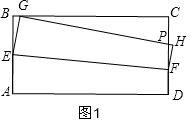 解:(1)如图1,由折叠得:EG=AE=y,则BE=2-y,
解:(1)如图1,由折叠得:EG=AE=y,则BE=2-y,
∵四边形ABCD为矩形,
∴∠B=90°,
由勾股定理得:EG2=BE2+BG2,
y2=(2-y)2+x2,
∴y=$\frac{1}{4}{x}^{2}$+1,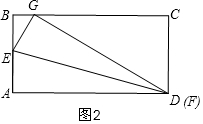
如图2,当F与D重合时,BG的值最大,
由折叠得:DG=AB=4,
在Rt△DGC中,DC=2,
CG=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴x=AE=4-2$\sqrt{3}$,
∴y关于x的关系式为:y=$\frac{1}{4}{x}^{2}$+1(0≤x≤4-2$\sqrt{3}$);
(2)如图1,∵∠EGP=90°,
∴∠BGE+∠PGC=90°,
∵∠B=90°,
∴∠BGE+∠BEG=90°,
∴∠PGC=∠BEG,
∵∠B=∠C=90°,
∴△BEG∽△CGP,
∴$\frac{BG}{CP}=\frac{BE}{CG}$,
∴$\frac{x}{CP}=\frac{2-y}{4-x}$,
∴CP=$\frac{x(4-x)}{2-y}$,
∴FP=CD-DF-CP=2-z-$\frac{x(4-x)}{2-y}$,
同理得:△BEG∽△HFP,
∴$\frac{BE}{HF}=\frac{EG}{FP}$,
∴BE•FP=FH•EG,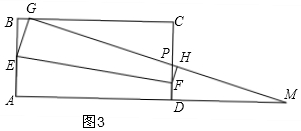
∴(2-y)•[2-z-$\frac{x(4-x)}{2-y}$]=yz,
z=$\frac{1}{4}{x}^{2}-2x+1$;
(3)存在,使直线GP和直线AD的夹角为30°,如图3,
∵∠PMD=30°,
∴∠DPM=60°,
∴∠GPC=∠DPM=60°,
∵∠C=90°,
∴∠PGC=30°,
∵∠EGP=90°,
∴∠BGE=60°,
∴∠BEG=30°,
∴EG=2BG,
即y=2x,
由(1)得:y=$\frac{1}{4}{x}^{2}$+1,
∴$\frac{1}{4}{x}^{2}$+1=2x,
解得:x1=4+2$\sqrt{3}$>4(不符合题意,舍),x2=4-2$\sqrt{3}$,
∴当x=4-2$\sqrt{3}$时,直线GP和直线AD的夹角为30°.
点评 本题是四边形的综合题,考查了矩形、折叠的性质、相似三角形的性质和判定、勾股定理;熟练掌握折叠前后的两边相等,两角相等,利用相似列比例式或利用勾股定理列等式,与方程相结合,列函数关系式或一元二次方程求解.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:填空题
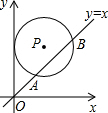 如图,在平面直角坐标系中,⊙P的圆心坐标是(4,a)(a>4),半径为4,函数y=x的图象被⊙P截得的弦AB的长为4$\sqrt{3}$,则a的值是4+2$\sqrt{2}$.
如图,在平面直角坐标系中,⊙P的圆心坐标是(4,a)(a>4),半径为4,函数y=x的图象被⊙P截得的弦AB的长为4$\sqrt{3}$,则a的值是4+2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
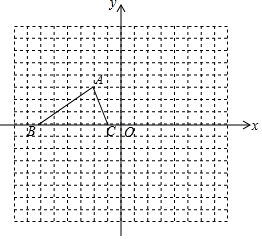 如图,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
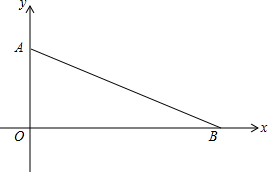 如图,在平面直角坐标系中,点A(0,7),B(24,0).△AOB内是否有一点P到各边的距离相等?如果有,请作出这一点,并求出符合条件的点P的坐标.
如图,在平面直角坐标系中,点A(0,7),B(24,0).△AOB内是否有一点P到各边的距离相等?如果有,请作出这一点,并求出符合条件的点P的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1组 | B. | 3组 | C. | 4组 | D. | 7组 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com