
| A. | 第一、三象限 | B. | 第二、三象限 | C. | 第二、四象限 | D. | 第三、四象限 |
分析 设反比例函数解析式为y=$\frac{k}{x}$(k≠0),由反比例函数图象上点的坐标特征可得出k=a2,分情况讨论即可得出结论.
解答 解:设反比例函数解析式为y=$\frac{k}{x}$(k≠0),
∵点P(a,a)在反比例函数图象上,
∴k=a2.
当a≠0时,k=a2>0,反比例函数图象在第一、三象限;
当a=0时,点P为原点,不可能在反比例函数图象上,故无此种情况.
故选A.
点评 本题考查了反比例函数图象上点的坐标特征以及反比例函数的性质,解题的关键是用a的值表示k的值.本题属于基础题,难度不大,解决该题型题目时,由点在函数图象上得出反比例函数系数k的取值范围是关键.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:解答题
 已知线段a,c(如图),用直尺和圆规作Rt△ABC,使∠C=Rt∠,BC=a,AB=c.(温馨提醒:1.请保留作图痕迹,不用写作法;2.如果用直尺和圆规无法作出符合条件的图形时,用三角板、量角器等工具画图,分数也可得5分)
已知线段a,c(如图),用直尺和圆规作Rt△ABC,使∠C=Rt∠,BC=a,AB=c.(温馨提醒:1.请保留作图痕迹,不用写作法;2.如果用直尺和圆规无法作出符合条件的图形时,用三角板、量角器等工具画图,分数也可得5分)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
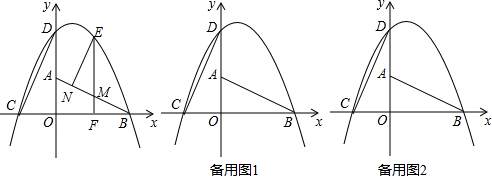
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
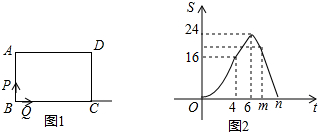
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com