
已知点A(1,![]() )在抛物线y=
)在抛物线y=![]() x2+bx+c上,点F(-
x2+bx+c上,点F(-![]() ,
,![]() )在它的对称轴上,点P为抛物线上一动点.
)在它的对称轴上,点P为抛物线上一动点.
(1)求这条抛物线的函数解析式;
(2)判断是否存在直线l,使得线段PF的长总是等于点P到直线l的距离,需说明理由.
(3)设直线PF与抛物线的另一交点为Q,探究:PF和QF这两条线段的倒数和是否为定值?证明你的结论.
.⑴ 由![]() =
=![]() ,a=
,a=![]() ,得b=
,得b=![]()
把b =![]() 和点A(1,
和点A(1,![]() )代入y=
)代入y=![]() x2+bx+c,可求得c=
x2+bx+c,可求得c=![]() .
.
∴这条抛物线的解析式是y=![]() x2+
x2+![]() x
x![]() .
.
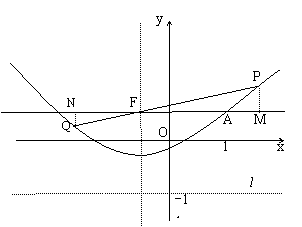 ⑵设点P(x0,y0),则y0=
⑵设点P(x0,y0),则y0=![]() x02+
x02+![]() x0
x0![]() .
.
作PM⊥AF于M,
得 PF2=PM2+MF2
= (x0+![]() )2+ (y0-
)2+ (y0-![]() )2
)2
又∵y0=![]() x02+
x02+![]() x0
x0![]()
=![]() (x0+
(x0+![]() )2-
)2-![]()
∴(x0+![]() )2=3y0+
)2=3y0+![]()
∴PF2=3y0+![]() + y02- y0+
+ y02- y0+![]() =( y0+1)2.
=( y0+1)2.
易知y0≥-![]() ,y0+1>0. ∴PF= y0+1.
,y0+1>0. ∴PF= y0+1.
又∵当直线l经过点(0,-1)且与x轴平行时,
y0+1即为点P到直线l的距离.
∴存在符合题意的直线l.
⑶ 是定值.
证明:当PF∥x轴时,PF=QF=![]() ,
,![]() .
.
当PF与x轴不平行时,作QN⊥AF于N,
∵ △MFP∽△NFQ,∴![]() .
.
再依据第⑵小题的结果,可得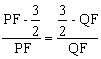 .
.
整理上式,得 ![]() .
.


科目:初中数学 来源: 题型:
| ||
| 2 |
 直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.
直高度为3.5米,C点与O点的水平距离为7米,以O为坐标原点,水平方向与竖直方向分别为x轴、y轴,建立直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +0.6 | -0.4 | -0.2 | +0.5 | +0.3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 男生的抛球处A点坐标为(0,2),实心球在空中线路的最高点B点的坐标是(6,5).
男生的抛球处A点坐标为(0,2),实心球在空中线路的最高点B点的坐标是(6,5).| 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

|
| t(秒) | 1 | 2 | 3 | … |
| x(米) | 20 | 40 | 60 | … |
| Y(米) | 5 | 20 | 45 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com