
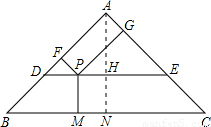
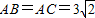 ,经过这个三角形重心的直线DE∥BC,分别交边AB、AC于点D和点E,P是线段DE上的一个动点,过点P分别做PM⊥BC,PF⊥AB,PG⊥AC,垂足分别为点M、F、G.设BM=x,四边形AFPG的面积为y.
,经过这个三角形重心的直线DE∥BC,分别交边AB、AC于点D和点E,P是线段DE上的一个动点,过点P分别做PM⊥BC,PF⊥AB,PG⊥AC,垂足分别为点M、F、G.设BM=x,四边形AFPG的面积为y.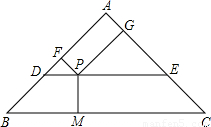
 BC=3,
BC=3, =2,
=2,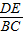 =
=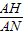 =
= ,
, AN=1,DE=4,
AN=1,DE=4,
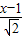 ,PG=
,PG=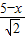 ,
,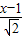 ×
× =
= (x-1)(5-x)=
(x-1)(5-x)=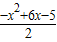 ,
,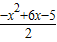 ,(1<x<5).
,(1<x<5).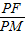 =
= ,即
,即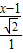 =
=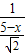 ,
,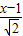 =
=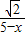 ,
, .
. .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com