
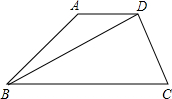
 已知:如图所示,梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=BC=4
已知:如图所示,梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=BC=4 ,求梯形的面积.
,求梯形的面积.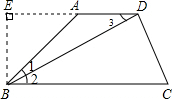 解:方法一:过点B作BE⊥DA交DA的延长线于E.
解:方法一:过点B作BE⊥DA交DA的延长线于E. ,
, BD=2
BD=2 ,ED=BD×cos30°=6.
,ED=BD×cos30°=6. ×
× =2,
=2,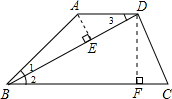
 (AD+BC)•EB=
(AD+BC)•EB= ×(4+4
×(4+4 )×2
)×2 =4
=4 +12.
+12. ,
, BD=2
BD=2 .
.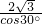 =4,
=4, BD=2
BD=2 ,
, (AD+BC)•DF=
(AD+BC)•DF= ×(4+4
×(4+4 )×2
)×2 =4
=4 +12.
+12.

科目:初中数学 来源:《24.4 中位线》2010年同步练习(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:《第1章 图形与证明(二)》2009年综合水平测试卷(A卷)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com