Question

18．已知，∠EPF的角平分线上有一点O，以点0为圆心的圆与角的两边分别交于A，B和C，D．易证：AB=CD．
当点P在⊙O外（如图二），点P在⊙O内，（如图三）的位置时，请你猜想并写出AB与CD的数量关系？并选择其中一种情况加以证明．

Answer 1

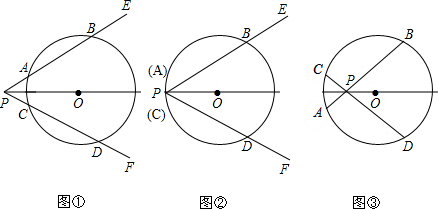
分析 对于图②：作OG⊥AB于G，OH⊥CD于H，连结OB、OD，根据垂径定理得到AG=BG，CH=DH，再根据角平分线的性质得OG=OH，然后证明Rt△OBG≌Rt△ODH得到BG=DH，则AB=CD；
对于图③：作OG⊥AB于G，OH⊥CD于H，则AG=GB，CH=HD，证明的方法与图②一样．

解答 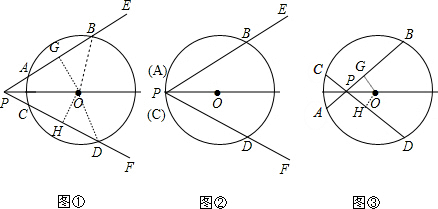解：AB=CD．理由如下：
对于图②：作OG⊥AB于G，OH⊥CD于H，连结OB、OD，则AG=BG，CH=DH，
∵PO平分∠EPF，
∴OG=OH，
在Rt△OBG和△ODH中，
$\left\{\begin{array}{l}{OB=OC}\\{OG=OH}\end{array}\right.$，
∴Rt△OBG≌Rt△ODH（HL），
∴BG=DH，
∴AB=CD；
对于图③：作OG⊥AB于G，OH⊥CD于H，则AG=GB，CH=HD，证明的方法与图②一样．

点评 本题考查了垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了角平分线的性质和全等三角形的判定．