
已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.
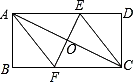
(1)求证:四边形AFCE是菱形;
(2)若AE=10 cm,△ABF的面积为24 cm2,求△ABF的周长;
(3)在线段AC上是否存在一点P,使得2AE2=AC·AP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.
|
本题满分12分 解:(1)证明:由题意可知OA=OC,EF⊥AO ∵AD∥BC ∴∠AEO=∠CFO,∠EAO=∠FCO ∴△AOE≌△COF ∴AE=CF,又AE∥CF ∴四边形AECF是平行四边形 2分 ∵AC⊥EF ∴四边形AECF是菱形 4分 (2)∵四边形AECF是菱形 ∴AF=AE=10 cm 设AB=a,BF=b, ∵△ABF的面积为24 cm2 a+b=100,ab=48 6分 (a+b)=196a+b=14或a+b=-14(不合题意,舍去) 7分 △ABF的周长为a+b+10=24 cm 8分 (3)存在,过点E作AD的垂线,交AC于点P,点P就是符合条件的点 9分
证明:∵∠AEP=∠AOE=90°,∠EAO=∠EAP ∴△AOE∽△AEP ∴ ∴AE=AO·AP 11分 ∵四边形AECF是菱形, ∴AO=AC ∴AE=AC·AP ∴2AE=AC·AP 12分 |


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
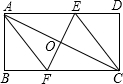 痕EF交AD边于E,交BC边于F,分别连接AF、CE和EF,设EF与AC的交点为O.
痕EF交AD边于E,交BC边于F,分别连接AF、CE和EF,设EF与AC的交点为O.| 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•乐清市模拟)已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连接AF和CE.
(2013•乐清市模拟)已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连接AF和CE.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.
已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.求证:四边形AFCE是菱形.
已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.求证:四边形AFCE是菱形.查看答案和解析>>
科目:初中数学 来源: 题型:
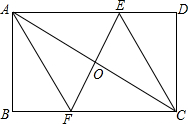 已知:如图所示的一张矩形纸片ABCD(AD>AB),O是对角线AC的中点,过点O的直线EF⊥AC交AD边于E,交BC边于F.
已知:如图所示的一张矩形纸片ABCD(AD>AB),O是对角线AC的中点,过点O的直线EF⊥AC交AD边于E,交BC边于F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com