Question

6．如图，直线DE与直线DF交于点D，△ABC与△A′B′C′关于DE对称．
（1）作△A′B′C关于直线DF对称的△A″B″C″；
（2）试探索∠BDB″与∠EDF之间的关系，并加以证明．

Answer 1

分析 （1）分别作出点A′、B′、C′关于直线DF的对称点A″、B″、C″即可得到△A″B″C″；
（2）理由对称的性质得∠BDE=∠B′DE，∠B′DG=∠B″DG，利用周角定理得到∠BDB″=360°-（∠BDE-∠B′DE-∠B′DG-∠B″DG），然后利用等量代换可得∠BDB″=360°-2∠EDG，再利用邻补角定义可得到∠BDB″与∠EDF之间的关系．

解答 解：（1）如图，△A″B″C″为所求；
（2）∠BDB″=2∠EDF．理由如下：
∵△ABC与△A′B′C′关于DE对称．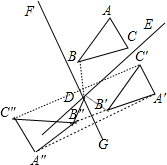
∴∠BDE=∠B′DE，
∵△A′B′C与△A″B″C″关于DF对称，
∴∠B′DG=∠B″DG，
∴∠BDB″=360°-（∠BDE-∠B′DE-∠B′DG-∠B″DG）
=360°-（2∠B′DE-2∠B′DG）
=360°-2∠EDG
=360°-2（180°-∠EDF）
=2∠EDF．

点评 本题考查了作图-轴对称变换：几何图形都可看做是有点组成，我们在画一个图形的轴对称图形时，可以确定一些特殊的对称点．也考查了对称轴的性质．