
 如图所示,已知菱形OABC,点C在x轴上,直线y=x经过点A,菱形OABC的面积是
如图所示,已知菱形OABC,点C在x轴上,直线y=x经过点A,菱形OABC的面积是 .若反比例函数的图象经过点B,则此反比例函数表达式为
.若反比例函数的图象经过点B,则此反比例函数表达式为

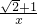
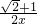
 a,由菱形的性质可得到AO=CO=CB=AB=
a,由菱形的性质可得到AO=CO=CB=AB= a,再利用菱形的面积公式计算出a的值,进而得到A点坐标,则可求得B点坐标,再利用待定系数法求出反比例函数表达式.
a,再利用菱形的面积公式计算出a的值,进而得到A点坐标,则可求得B点坐标,再利用待定系数法求出反比例函数表达式. a,
a, a,
a, ,
, a•a=
a•a= ,
, ,A(1,1)
,A(1,1) +1,1),
+1,1), (k≠0),
(k≠0), +1)×1=
+1)×1= +1,
+1,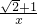 ,
,

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com