
(11·钦州)(本题满分12分).
如图,在平面直角坐标系中,抛物线与x轴交于A、B两点(A在B的左侧),与y轴交于点C (0,4),顶点为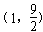 .
.
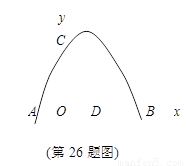
(1)求抛物线的函数表达式;
(2)设抛物线的对称轴与轴交于点D,试在对称轴上找出点P,使△CDP为等腰三角形,请直接写出满足条件的所有点P的坐标.
(3)若点E是线段AB上的一个动点(与A、B不重合),分别连接AC、BC,过点E作EF∥AC交线段BC于点F,连接CE,记△CEF的面积为S,S是否存在最大值?若存在,求出S的最大值及此时E点的坐标;若不存在,请说明理由.
(1)∵抛物线的顶点为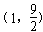
∴设抛物线的函数关系式为y=a (
x-1) 2+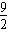 ………………2分
………………2分
∵抛物线与y轴交于点C (0,4),
∴a (0-1)
2+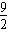 =4
=4
解得a=-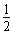
∴所求抛物线的函数关系式为y=-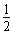 ( x-1)
2+
( x-1)
2+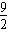 ………………4分
………………4分
(2)解: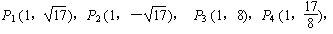 ,
………………8分
,
………………8分
(3)解:令-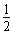 ( x-1)
2+
( x-1)
2+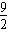 =0,解得x1=-2,x1=4
=0,解得x1=-2,x1=4
∴抛物线y=-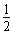 ( x-1)
2+
( x-1)
2+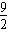 与x轴的交点为A (-2,0) C (4,0) ………………9分
与x轴的交点为A (-2,0) C (4,0) ………………9分
过点F作FM⊥OB于点M,
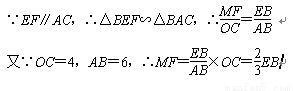
设E点坐标为 (x,0),则EB=4-x,MF=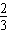 (4-x)
…………10分
(4-x)
…………10分
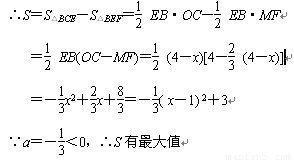
当x=1时,S最大值=3 …………11分
此时点E的坐标为 (1,0) …………12分
【解析】略


科目:初中数学 来源: 题型:
(11·钦州)(本题满分9分)
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.
(1)求证:AC平分∠DAB;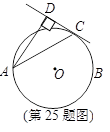
(2)过点O作线段AC的垂线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作法);
(3)若CD=4,AC=4,求垂线段OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
(11·钦州)(本题满分8分)
某校教学楼后面紧邻着一个山坡,坡上面是一块平地,如图所示,BC∥AD,BE⊥AD,斜坡AB长为26米,坡角∠BAD=68°.为了减缓坡面防止山体滑坡,保障安全,学校决定对该斜坡进行改造,经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.

(1)求改造前坡顶到地面的距离BE的长(精确到0.1米);
(2)如果改造时保持坡脚A不动,坡顶B沿BC向左移11米到F点处,问这样改造能确保安全吗?
(参考数据:sin 68°≈0.93,cos 68°≈0.37,tan 68°≈2.48,sin 58°12’≈0.85,tan 49°30’≈1.17)
查看答案和解析>>
科目:初中数学 来源: 题型:
(11·钦州)(本题满分9分)
某生姜种植基地计划种植A、B两种生姜30亩.已知A、B两种生姜的年产量分别为2 000千克/亩、2 500千克/亩,收购单价分别是8元/千克、7元/千克.
(1)若该基地收获两种生姜的年总产量为68 000千克,求A、B两种生姜各种多少亩?
(2)若要求种植A种生姜的亩数不少于B种的一半,那么种植A、B两种生姜各多少亩时,全部收购该基地生姜的年总收入最多?最多是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
(11·钦州)(本题满分9分)
某校为了解九年级800名学生的体育综合素质,随机抽查了50名学生进行体育综合测试,所得成绩整理分成五组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题:
频数分布表 扇形统计图
| 组别 | 成绩(分) | 频数 |
| A | 50≤x<60 | 3 |
| B | 60≤x<80 | m |
| C | 70≤x<80 | 10 |
| D | 80≤x<90 | n |
| E | 90≤x<100 | 15 |
(1)频数分布表中的m=_ ▲ ,n=_ ▲ ;
(2)样本中位数所在成绩的级别是_ ▲ ,扇形统计图中,E组所对应的扇形圆心角的度数是_ ▲ ;
(3)请你估计该校九年级的学生中,体育综合测试成绩不少于80分的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
(11·钦州)(本题满分7分)
如图,在平面直角坐标系中,点O为原点,反比例函数y=的图象经过点(1,4),菱形OABC的顶点A在函数的图象上,对角线OB在x轴上.
(1)求反比例函数的关系式;
(2)直接写出菱形OABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com